Próxima: Algumas Relações Termodinâmicas Volta: Interiores Estelares Anterior: Equilíbrio Hidrostático

Reserva de Energia de uma Estrela

Assegurar equilíbrio hidrostático não é suficiente para assegurar a estabilidade de uma estrela. O equilíbrio térmico também precisa ser considerado. Um equilíbrio térmico perfeito só é atingido por um sistema se todas as partes têm a mesma temperatura, e não existe qualquer fluxo de energia entre suas partes. Este equilíbrio perfeito certamente não ocorre no interior de uma estrela. Vimos que a temperatura no interior do Sol é da ordem de 15 milhões de graus, enquanto a temperatura nas camadas superficiais é da ordem de 5400 K. Além disto, medimos um fluxo de energia saindo das camadas superficiais, L^⊙=3,838×10³³ergs/s, a luminosidade do Sol. Como L_ν^⊙≃0,023 L^⊙, (L^⊙+L_ν^⊙)/c²=4,36×10¹²g/s=6,92×10^-8M_⊙/M ano, maior do que a perda por vento solar (M_vento^⊙≃1,2×10¹²g/s≃2,0×10^-8M_⊙/M ano). A existência deste fluxo significa desvio do equilíbrio térmico perfeito. Mas as estrelas conseguem manter equilíbrio térmico, com um perfil de temperatura T(r) constante, se tiverem uma fonte de energia para compensar a perda de energia pela luminosidade total.

Que tipo de equilíbrio térmico atua no interior de uma estrela? Para responder esta pergunta, precisamos primeiro encontrar as fontes de energia que mantém o fluxo através da superfície (fotosfera). Precisamos considerar três tipos de energia: energia térmica, 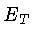, energia gravitacional, , e energia nuclear, . As duas primeiras podem ser representadas por uma simples integral sobre a estrela. Para o Sol

$E_T = \int_0^R (+ \frac{3}{2}\frac{k}{m}T ) \rho 4\pi ...\overline{\frac{3k}{2m}T} \times M_\odot \approx +5 \times 10^{48} ergs$

(1.26)

$E_G = \int_0^R (- \frac{GM_r}{r}) \rho 4 \pi r^2 dr = - \overline{\frac{GM_r}{r}} \times M_\odot \approx -4 \times 10^{48}\,{\rm ergs}.$

(1.27)

O termo em parêntesis na equação (1.26) representa a energia térmica de um gás ideal, monoatômico, por grama de matéria, enquanto o termo em parêntesis na equação (1.27) representa a energia necessária para mover uma grama de matéria de sua posição na estrela até o infinito, depois que todas as outras camadas externas da estrela já foram removidas. O valor numérico cotado nas equações é uma estimativa da ordem de grandeza das duas energias, usando os valores médios para o Sol.

Não é por acidente que as estimativas das duas energias são tão parecidas. A igualdade segue diretamente da equação de equilíbrio hidrostático; multiplicando a equação de equilíbrio hidrostático (1.24)

$\frac{dP}{dr}=-\rho \frac{GM_r}{r^2}$

(1.24)

por 4π r³dr e integrando sobre a estrela, obtemos:

$\int_0^R dP \times 4\pi r^3 = -\int_0^R GM_r 4\pi r dr.$

Integrando por partes o termo da esquerda, isto é:

$\int udv = uv - \int vdu,$

e usando u=4π r³ e dv=dP, obtemos:

$\int_0^R 4\pi r^3 dP = P 4\pi r^3\Big\bracevert_0^R - \int^R_0 3P 4\pi r^2 dr.$

O primeiro termo à direita pode ser desprezado porque no interior o raio é nulo, e na superfície a pressão é insignificante. Logo

${\int_0^R 3P 4\pi r^2dr = \int_0^R \frac{GM_r}{r} 4\pi r^2dr,}$$

(1.28)

que é o Teorema do Virial da dinâmica clássica, ou virial de Clausius, em honra ao seu proponente, o alemão Rudolf Julius Emanuel Clausius (1822-1888). Identificando o termo da direita com o negativo da energia gravitacional,

, e usando a equação de estado de um gás ideal (1.25) $P=\frac{\rho}{m}kT$ :

$\int_0^R 3P 4\pi r^2 dr = 2 \int_0^R \frac{3}{2}\frac{kT}{m} \rho 4\pi r^2dr = 2 E_T,$

obtemos:

${2 E_T = -E_G.}$

(1.29)

Naturalmente os valores obtidos nas equações (1.26) e (1.27) não são exatamente múltiplos, pois são apenas estimativas de grandeza.

Para uma estrela não degenerada em contração, a energia gravitacional decresce continuamente. Exatamente metade deste decréscimo de energia será compensado por um aumento na energia térmica, de acordo com a relação (1.29). A outra metade será perdida por radiação pela superfície. Desta forma, a quantidade de energia passível de perda por radiação é somente igual à energia térmica. Por quanto tempo esta reserva de energia pode suprir a energia irradiada pela superfície? Nossas estimativas numéricas para o Sol podem ser usadas para calcular este tempo, chamado de tempo de contração de Kelvin,

$t_K = \frac{E_T^\odot}{L_\odot} \approx 10^{15}\,{\rm s} = 3 \times 10^7\,{\rm anos},$

já que L_⊙=3,838×10³³ergs/s. Este tempo, também chamado de tempo de Kelvin-Helmholtz, em honra ao irlandês Lord William Thomson, Barão Kelvin (1824-1907), e ao alemão Hermann Ludwig Ferdinand von Helmholtz (1821-1894), é muito curto, mesmo se comparado com o intervalo de tempo desde o aparecimento de algas na Terra. Portanto concluímos que a energia térmica e gravitacional de uma estrela não são suficientes para suprir a perdas pela superfície durante a vida de uma estrela, embora possam ser importantes em fases curtas e críticas da evolução estelar.

Nesta derivação, a energia térmica, E_T, foi definida como a energia cinética translacional, e não inclui a energia dos graus de liberdade internos, como rotação, vibração ou excitação. Do virial, obtemos:

$E_\mathrm{total} = E_T + E_G = \frac{1}{2}E_G.$

Esta relação, e (1.29), só são estritamente válidas para um gás em que o coeficiente adiabático, $\gamma =\frac{5}{3}$ , onde

$\boxed {\gamma \equiv \frac{c_p}{c_v},}$

e c_p e c_v são os calores específicos a pressão constante e a volume constante, como a equação do gás ideal. O conceito de calor específico foi desenvolvido por Joseph Black (1728-1799). Para uma equação de estado adiabática - sem perda de calor - geral, definida como:

$d\ln P \equiv \gamma d\ln \rho,$

e como derivaremos na próxima seção (eq. 1.32-16):

$P = (\gamma-1)\rho E_T^{part.},$

(1.30)

podemos calcular a energia cinética total do gás K, já que p=mv e:

$K \equiv \sum_i \frac{1}{2}m_i v_i^2 = \frac{1}{2}\sum_i \vec{p_i}\cdot \vec{v_i}.$

Para um gás isotrópico, como vimos na equação (1.7)

$P=\frac{1}{3}\int_p n(p)\vec{p_i}\cdot \vec{v_i} d^3p.$

Portanto, se integramos sobre o volume, para incluir todas as partículas,

$2K=3\int_V PdV$

(1.31)

Usando

$dM_r=\rho d\left(\frac{4}{3}\pi r^3\right),$

$2K=3\int_M \frac{P}{\rho}dM_r,$

(1.31a)

e o teorema de virial da equação (1.28)

${\int_0^R 3P 4\pi r^2dr = \int_0^R \frac{GM_r}{r} 4\pi r^2dr,}$$

(1.28)

pode ser escrito como:

Como, substituindo-se P=(γ-1)ρE_T^part (1.30) em (1.31):

$2K=3(\gamma-1)\int_V\rho E_T^{part}dV = 3(\gamma-1)E_T,$

$K = \frac{3}{2}(\gamma-1)E_T,$

onde K é a energia cinética total. Desta forma, vemos que E_T=K somente se $\gamma =\frac{5}{3}$ . A energia total pode ser escrita como:

$E_\mathrm{total}$
		$\frac{2K}{3(\gamma-1)}+E_G$
		$-\frac{E_G}{3(\gamma-1)}+E_G$

e finalmente:

${E_\mathrm{total}=\frac{3\gamma-4}{3(\gamma-1)}E_G.}$

(1.32)

Para um gás de Fermi completamente relativístico, γ=4/3, e neste caso toda a variação de energia gravitacional transforma-se em energia interna, sem que a estrela precise irradiar. Como a energia total é dada por (1.32), se γ=4/3 a energia total é deixa de ser negativa, e massa é perdida pela estrela - camadas externas são ejetadas. Como γ=4/3 também para fótons, uma estrela dominada pela pressão de radiação efetivamente ejecta suas camadas externas. Este fato é o que limita a massa superior das estrelas, próximo de 100 M_⊙, para metalicidade solar. A ionização também pode fazer γ decrescer abaixo de 4/3 nas regiões de ionização, causando instabilidades, como pulsações.

Próxima: Algumas Relações Termodinâmicas Volta: Interiores Estelares Anterior: Equilíbrio Hidrostático

Astronomia e Astrofísica