Próxima: Pressão Mecânica Volta: Interiores Estelares Anterior: Interiores Estelares

O Sol

Massa	M_⊙ = 1,9884×10³⁰ kg
Raio	R_⊙ = 695 500 km = 109 R_Terra
Densidade média	ρ = 1409 kg/m³
Densidade central	ρ_c= 160 000 kg/m³
Distância	1 UA = 149 600 000 km
Luminosidade	L_⊙=3,828×10²⁶ watts=3,828×10³³ ergs/s
Luminosidade em neutrinos	L_ν^⊙≃0,023 L_⊙
Temperatura efetiva	T_ef^⊙ = 5785 K
Temperatura central	T_c^⊙ = 15 000 000 K
Magnitude absoluta bolométrica	M_bol^⊙ = 4,72
Magnitude absoluta visual	M_V^⊙ = 4,79
Tipo espectral e classe de luminosidade	G2 V
Índices de cor	B-V=0,62
	U-B=0,10
Composição química principal (N^o)	Hidrogênio = 91,2 %
	Hélio = 8,7%
	Oxigênio = 0,078 %
	Carbono = 0,043 %
Período rotacional no equador	25,67 d
na latitude 45°	27,50 d
na latitude 75°	33,40 d

Equação de Estado

Uma equação de estado é uma equação termodinâmica relacionando os parâmetros da matéria, como temperatura, pressão, densidade e energia interna. Não existe uma única equação de estado que descreva as propriedades sob todas as condições. Uma equação de estado clássica é a equação do gás ideal, formulada historicamente pelo inglês Robert Boyle (1627-1691) em 1662, que descreve adequadamente gases atômicos e moleculares. 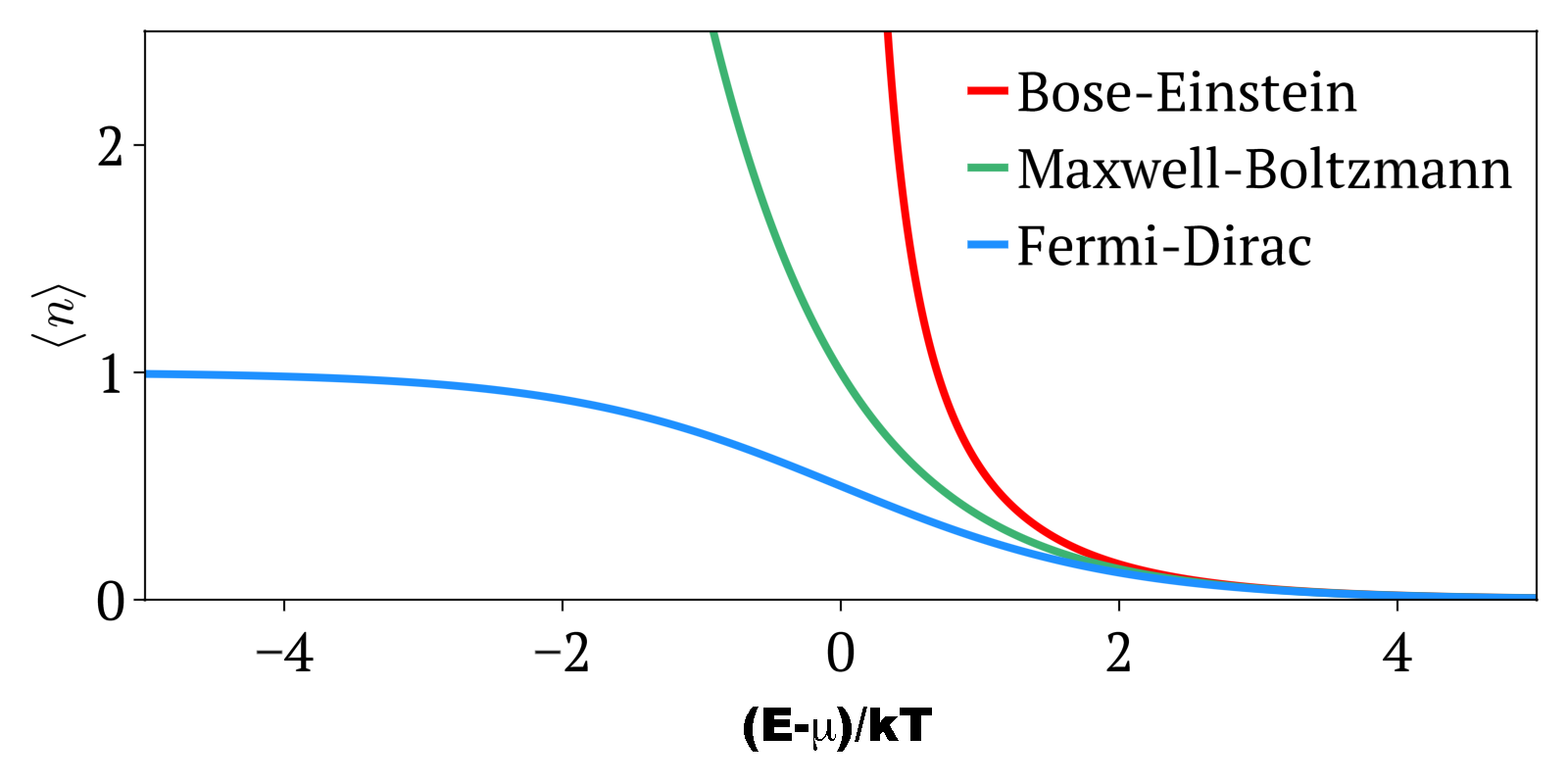Para partículas elementares precisamos levar em conta suas massas e spin, com a estatística de Fermi-Dirac, para spins semi-inteiros ou Bose-Einstein, para spins inteiros.

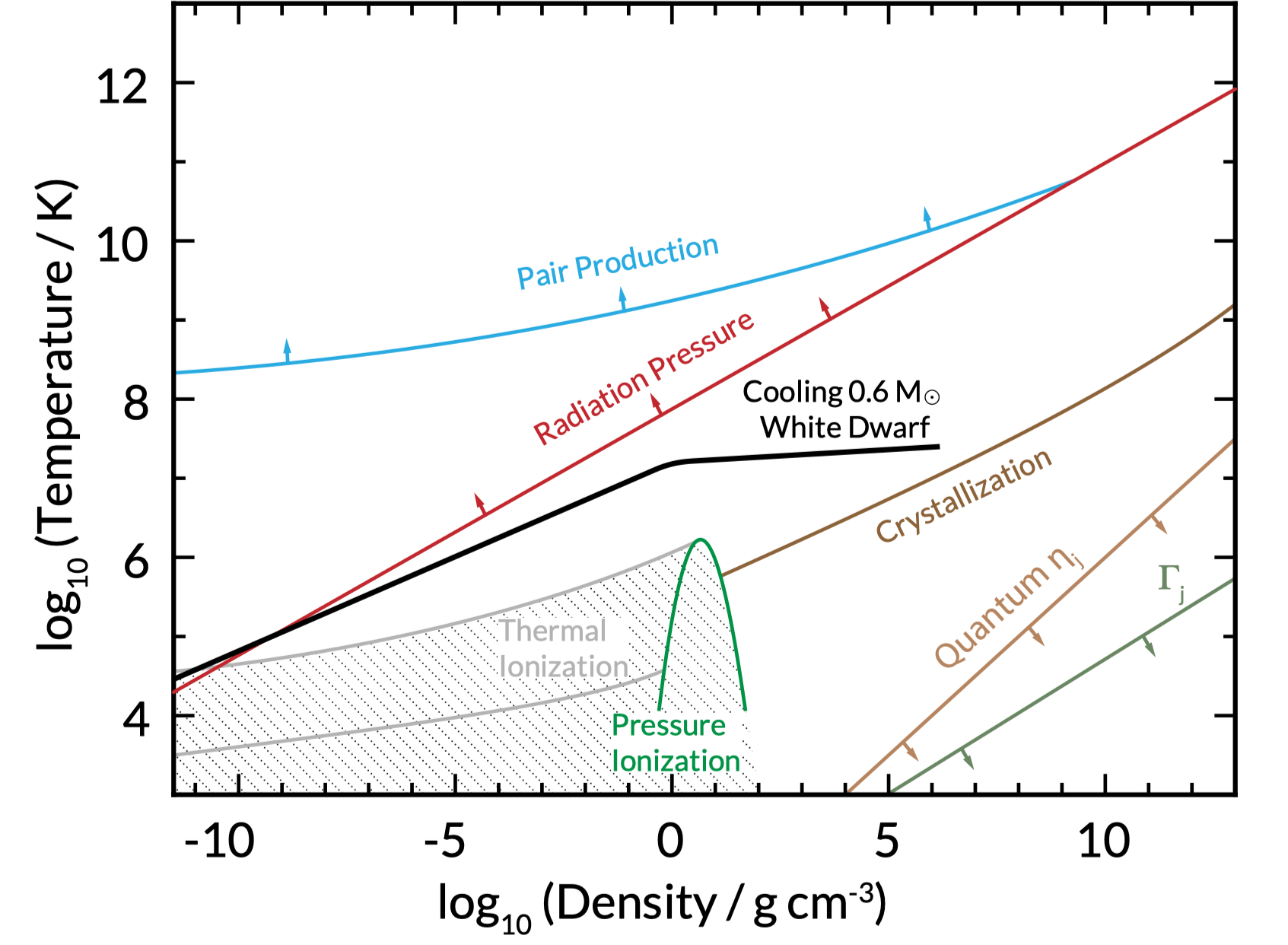Tabelas para matéria ionizada para uso em modelos, incluindo escudamento eletrônico, cristalização, efeitos relativísticos para 10^-12 g/cm³≥ρ≥10¹³ g/cm³ e 10³ K≥ T ≥10¹³ K foram calculadas por Adam S. Jermyn, Josiah Schwab, Evan Bauer, Frank X. Timmes & Alexander Y. Potekhin, Skye: A Differentiable Equation of State, 2021, Astrophysical Journal, 913, id 72.

Temperatura

O conceito físico de temperatura está associado ao conceito de equilíbrio térmico, pois é uma medida da energia cinética média das partículas. Um sistema mecânico tem muitas configurações possíveis, dependendo da distribuição de energia de seus subsistemas. Dentre estas configurações, existe aquela mais provável, em que todos os subsistemas estão em equilíbrio térmico, e que pode ser calculada com as técnicas da mecânica estatística de equilíbrio. Em equilíbrio térmico existe balanço detalhado: todo processo microscópico é exatamente balançado pelo processo inverso. Como o assunto envolve resultados de tratamento detalhados de muitos campos da física, aqui simplesmente citaremos os resultados, e justificaremos com argumentos qualitativos, deixando a demonstração para textos especializados.

Em um sistema clássico, as partículas se movem em trajetórias definidas, de modo que podemos, em princípio, distingüir entre as partículas, mesmo idênticas, isto é, podemos colocar rótulos de partícula 1, partícula 2, ... Em uma descrição quântica isto não pode ser feito porque o Princípio da Incerteza de Heisenberg, que rendeu o prêmio Nobel em física de 1932 ao físico alemão Werner Karl Heisenberg (1901-1976), não permite a contínua observação do movimento das partículas, sem mudar o comportamento do sistema. Isto é equivalente a dizer que, em mecânica quântica, que descreve as partículas como ondas tridimensionais, onde a função de onda associada a cada partícula não é pontual e dá a probabilidade de se encontrar a partícula em uma posição, a superposição da função de onda torna impossível a distinção entre as partículas. Portanto, em uma descrição quântica, as partículas idênticas são indistingüíveis.

Partículas descritas por autofunções assimétricas têm spin semi-inteiro, e são chamadas de férmions, em honra ao físico ítalo-americano Enrico Fermi (1901-1954), e estão sujeitas ao Princípio da Exclusão, elaborado pelo físico austríaco Wolfgang Pauli (1900-1958), e que lhe rendeu o prêmio Nobel em 1945: duas partículas de mesmo spin não podem ocupar o mesmo estado quântico.

As partículas de Bose, ou bósons, em honra ao físico indiano Satyendra Nath Bose (1894-1974), têm spin inteiro, e embora indistingüíveis, não estão sujeitas ao Princípio da Exclusão, porque têm autofunções simétricas, que não se anula se todos os números quânticos de duas ou mais partículas forem idênticos.

Para um gás em equilíbrio, a configuração mais provável depende da natureza das partículas do gás, que para partículas elementares caem em três classes:
1) partículas idênticas mas distingüíveis, que são as partículas clássicas;
2) partículas idênticas mas indistingüíveis de spin semi-inteiro, por exemplo, elétrons, pósitrons, neutrinos, prótons, nêutrons e mésons μ; e
3) partículas idênticas mais indistingüíveis de spin inteiro, por exemplo fótons, mésons π e partículas α (He⁴).

Se o número de partículas com momentum p é definido como n(p), e o número de estados possíveis de momentum p por g(p), a configuração mais provável, a função partição, correspondendo a estes três casos pode ser derivada pela mecânica estatística, maximizando-se o número de maneiras de distribuir as partículas nos níveis de energia disponíveis:

${n(p)dp = \frac{g(p)}{e^{(E-\mu)/kT}+0}dp}$	estatística de Maxwell-Boltzmann	(1.1)
${n(p)dp = \frac{g(p)}{e^{(E-\mu)/kT}+1}dp}$	estatística de Fermi-Dirac	(1.2)
$n(p)dp = \frac{g(p)}{e^{(E-\mu)/kT}-1}dp$	estatística de Bose-Einstein	(1.3)

A energia E nas equações acima é a energia de cada partícula. O parâmetro μ, o potencial químico, definido como [seção (1.4.1)]

$\mu = (\frac{\partial E_{gas}}{\partial N})_{s,v}$

onde s é a entropia e v o volume. O potencial químico é um multiplicador Lagrangeano dependente da densidade de partículas - a energia adicionada ao sistema quando uma partícula é introduzida no sistema -, e é obtido através da normalização

$N=\int_0^\infty n(p)dp$

onde N é a densidade total de partículas - número de partículas por unidade de volume - e onde E_gás é a densidade de energia total do gás. O conceito de potencial químico foi introduzido pelo físico-químico americano Josiah Willard Gibbs (1839-1903). Estas fórmulas são derivadas considerando-se as várias maneiras de se arranjar um número fixo de partículas em estados individuais de energia, de modo que a energia total do gás seja conservada.

Na estatística de Fermi-Dirac, derivada por Enrico Fermi e pelo inglês Paul Adrien Maurice Dirac (1902-1984),

$\mu\equiv E_F(T)$

para T=0, onde E_F é chamada de energia de Fermi, e depende fracamente da temperatura. A Energia de Fermi é o valor da energia cinética para o estado mais alto ocupado pelos férmions em um sistema.

Para um gás de fótons, que são bósons de massa zero, μ=0, porque o número de fótons não é conservado, isto é, quanto maior é a temperatura - energia -, maior é o número de fótons.

A densidade de estados livres, ou fator de degenerescência g(p) pode ser derivada usando-se o princípio da incerteza de Heisenberg

$\Delta p_i \Delta x_i \geq h$

e o fato de que para elétrons e para fótons podem existir dois estados de polarização (spin), e que o volume do espaço de momentum, para o qual o vetor $\vec{p}$ tem magnitude constante p, é simplesmente o volume da casca esférica, 4πp²dp:

$g(p)dp = \frac{2}{h^3}4\pi p^2dp$

para fótons e elétrons. ^1.1

Para temperatura zero,

$E_F = \frac{h^2}{8m}(\frac{3N}{\pi})^{2/3}$

(1.4)

onde h é a constante de Planck, com valor h=6,63×10^-27 ergs s, e m é a massa da partícula. Todos os estados com $E\leq E_F$ estão ocupados, e todos os estados com

estão desocupados. Esta relação pode ser derivada da equação (1.2), já que, para T=0,

$N=\int_0^{p_F} \frac{2}{h^3} 4\pi p^2 dp=\frac{8\pi}{3h^3}p_F^3$

logo

$p_F=\frac{h}{2}(\frac{3N}{\pi})^\frac{1}{3}$

e considerando que para temperatura zero podemos usar a relação entre momentum e velocidade não relativística (p=mv)

$E_F=\frac{1}{2}m\frac{p^2}{m^2}=\frac{p^2}{2m}=\frac{h^2}{8m}(\frac{3N}{\pi})^{2/3}$

A relação entre a velocidade v e o momentum p depende de se o gás é relativístico ou não. Para um gás não relativístico (v≪c), onde c é a velocidade da luz, v=p/m. Para um gás relativístico,

$v \equiv \frac{\partial E_{part}}{\partial p}= \frac{p/m_0}{[1+(p/m_0c)^2]^{\frac{1}{2}}$

onde E_part é a energia da partícula e m_o é sua massa de repouso.

A densidade de energia do gás, isto é, energia por unidade de volume, será então dada por:

$E_{gas}=\int_0^\infty n(p)E(p)dp$

(1.5)

onde E(p) é a energia de cada partícula, como função do momentum.

O número de maneiras possíveis de configurar partículas idênticas em g estados é g!, e a aproximação de Stirling [James Stirling (1692-1770)] permite escrever o fatorial, para um grande número de estados, em termos de uma exponencial. O erro relativo é menor que 1% para cerca de 1000 partículas.

Próxima: Pressão Mecânica Volta: Interiores Estelares Anterior: Interiores Estelares