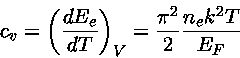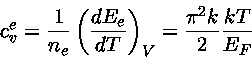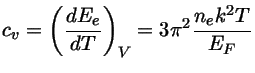Calor Específico dos Elétrons em um gás degenerado
Da definição de
pressão e
energia,
para um gás de férmions temos:
e que para um gás não relativístico
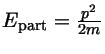 .
Definimos
e obtivemos para o caso da degenerescência parcial:
logo
Como a pressão do gás de elétrons degenerados mas não
relativísticos é dada por
e a densidade de elétrons dada por
com a energia de Fermi (sem a massa de repouso)
como vimos na equação (efermi/lista 54)
dada por
onde
é a energia de Fermi à temperatura zero. Se o gás está
degenerado, a energia de Fermi é muito maior do que kT e
Desta maneira
Expandindo os termos dependentes em temperatura em termos de
.
Definimos
e obtivemos para o caso da degenerescência parcial:
logo
Como a pressão do gás de elétrons degenerados mas não
relativísticos é dada por
e a densidade de elétrons dada por
com a energia de Fermi (sem a massa de repouso)
como vimos na equação (efermi/lista 54)
dada por
onde
é a energia de Fermi à temperatura zero. Se o gás está
degenerado, a energia de Fermi é muito maior do que kT e
Desta maneira
Expandindo os termos dependentes em temperatura em termos de
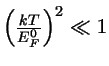 obtemos
e obtemos a capacidade térmica total dos elétrons a volume constante
para um gás degenerado mas não relativístico
e, portanto,
o calor específico por elétron:
obtemos
e obtemos a capacidade térmica total dos elétrons a volume constante
para um gás degenerado mas não relativístico
e, portanto,
o calor específico por elétron:
Para um gás degenerado e ultra-relativístico,



Volta: Evolução das Anãs Brancas
Volta: Evolução Estelar
Volta: Introdução à Astronomia e à Astrofisica
©kepler@if.ufrgs.br
Modificada em 17 out 2001
![$ P = \frac{8\pi}{3h^3}\int_0^\infty \frac{p^3v_pdp}{\exp[(E-E_Fg)/kT]+1}$](imgd1.gif)
![$ P = \frac{8\pi}{3h^3}\int_0^\infty \frac{p^3v_pdp}{\exp[(E-E_Fg)/kT]+1}$](imgd1.gif)
![$ n = \frac{8\pi}{3h^3}\int_0^\infty \frac{p^2dp}{\exp[(E-E_Fg)/kT]+1}$](imgd2.gif)
![$ E = \frac{8\pi}{3h^3}\int_0^\infty \frac{E_{part}p^2dp}{\exp[(E-E_Fg)/kT]+1}$](imgd3.gif)
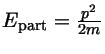 .
Definimos
.
Definimos
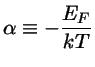
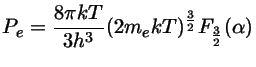
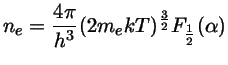
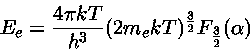
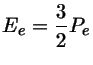
![P_e=\frac{2}{5}n_e E_F^0[1+\frac{5\pi^2}{12}(\frac{kT}{E_F^0})^2]$](img3.gif)
![n_e=\frac{32\pi(m E_F)^\frac{3}{2}}{3\sqrt{2}h^3}[1+\frac{\pi^2}{8}(\frac{kT}{E_F})^2]](img4.gif)
![\frac{1}{E_F}=\frac{1}{E_F^0}[1+\frac{\pi^2}{8}(\frac{kT}{E_F^0})^2]^\frac{3}{2}](img5.gif)
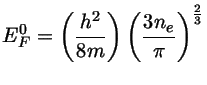
![$ E_F = E_F^0[1-\frac{\pi^2}{12}(\frac{kT}{E_F^0})^2]$](img7.gif)
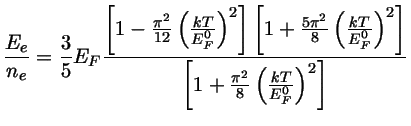
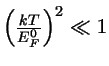 obtemos
obtemos
![$ E_e=\frac{3}{5}n_eE_F[1+\frac{5\pi^2}{8}(\frac{kT}{E_F^0})^2]$](img10.gif)