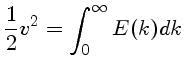Próxima: Aproximação Adiabática para dT/dr
Volta: Transporte de Energia por Convecção
Anterior: Equilíbrio Convectivo
Precisamos agora derivar uma relação entre o gradiente de
temperatura e o fluxo total de energia no estado
de equilíbrio convectivo. Para isto, precisamos considerar em detalhe
o transporte de energia dos elementos em movimento,
dentro da teoria do comprimento de mistura (mixing length theory),
desenvolvida pelos alemães
Ludwig Franz Benedikt Biermann (1907-1986) em 1948
(Konvektion in rotierenden Sternen,
Zeitschrift für Astrophysik, 25, 135),
Erika Vitense (1953,
Die Wasserstoffkonvektionszone der Sonne,
Zeitschrift für Astrophysik, 32, 135),
e Erika
Böhm-Vitense
(1958,
Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte,
Zeitschrift für Astrophysik, 46,108), baseados no trabalho do
alemão Ludwig Prandtl
(1875-1953) de 1925, considerado um dos pais da mecânica de fluidos
(Zeitschrift für Angewandte Mathematik und Mechanik, 5, 136).
O excesso de temperatura de um elemento ascendente sobre o
meio circundante é dado pela diferença entre a
mudança de temperatura adiabática, dentro do elemento,
e a mudança de temperatura real no meio,
desde o ponto de início do movimento até seu ponto final.
Se o elemento se deslocou uma distância 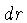 , seu excesso
de temperatura será:
, seu excesso
de temperatura será:
onde o símbolo:
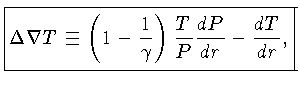 |
(1.55) |
representa o excesso do gradiente de temperatura real - em valor
absoluto - sobre o gradiente de temperatura adiabático. Se multiplicarmos
este excesso de temperatura por  , obtemos o excesso
de energia térmica por unidade de volume. Se ainda multiplicarmos
pela velocidade do elemento
, obtemos o excesso
de energia térmica por unidade de volume. Se ainda multiplicarmos
pela velocidade do elemento 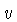 , obtemos o
fluxo de energia por unidade de área, por unidade de tempo:
, obtemos o
fluxo de energia por unidade de área, por unidade de tempo:
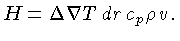 |
(1.56) |
Exatamente a mesma equação vale para o elemento descendente,
já que uma mudança de sinal em 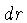 compensa uma mudança
em sinal em
compensa uma mudança
em sinal em 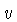 . De fato, a equação (1.56) representa
o fluxo médio produzido por movimentos convectivos se
. De fato, a equação (1.56) representa
o fluxo médio produzido por movimentos convectivos se 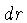 é tomado como o deslocamento médio (isto é, a distância
vertical a partir da camada em que o elemento tinha a mesma
temperatura interna do meio), e
é tomado como o deslocamento médio (isto é, a distância
vertical a partir da camada em que o elemento tinha a mesma
temperatura interna do meio), e 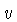 é tomada como a velocidade
média do deslocamento vertical de todos os elementos de uma camada.
é tomada como a velocidade
média do deslocamento vertical de todos os elementos de uma camada.
A equação (1.56) já representa a relação
necessária entre o transporte de energia convectivo e
o gradiente de temperatura. Não está, ainda, em uma
forma conveniente, já que a velocidade 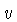 precisa ser
determinada primeiro pela seguintes considerações
dinâmicas. A deficiência de densidade do elemento ascendente
sobre o meio circundante pode ser calculada, similarmente
ao excesso de temperatura, pela seguinte fórmula, usando-se
a desigualdade (1.52):
precisa ser
determinada primeiro pela seguintes considerações
dinâmicas. A deficiência de densidade do elemento ascendente
sobre o meio circundante pode ser calculada, similarmente
ao excesso de temperatura, pela seguinte fórmula, usando-se
a desigualdade (1.52):
Se a deficiência de densidade é multiplicada pela aceleração
gravitacional, obtemos a deficiência em força gravitacional, ou
excesso de força para cima. Como esta força atua somente ao final
do deslocamento, a força média é obtida multiplicando-se
por 1/2. Multiplicando-se este excesso de força médio
pela distância 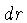 , obtemos o trabalho realizado
pelo excesso de força sobre o elemento. É este trabalho
que produz a energia cinética do elemento. Portanto:
, obtemos o trabalho realizado
pelo excesso de força sobre o elemento. É este trabalho
que produz a energia cinética do elemento. Portanto:
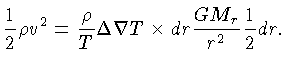 |
(1.57) |
Como os dois lados da equação (1.57) são quadráticos
em 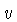 e
e 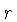 , ela vale para elementos ascendentes e descendentes.
Portanto, podemos tomar a equação (1.57)
como representativa de todos os elementos de uma camada, se novamente
tomarmos
, ela vale para elementos ascendentes e descendentes.
Portanto, podemos tomar a equação (1.57)
como representativa de todos os elementos de uma camada, se novamente
tomarmos 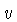 e
e 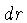 como representando médias apropriadas.
A equação (1.57) nos dá a velocidade de convecção
em termos do gradiente de temperatura. Ela pode ser utilizada
para eliminar a velocidade de convecção da
equação (1.56) do fluxo. Introduzimos aqui
um comprimento de mistura ( mixing length)
como representando médias apropriadas.
A equação (1.57) nos dá a velocidade de convecção
em termos do gradiente de temperatura. Ela pode ser utilizada
para eliminar a velocidade de convecção da
equação (1.56) do fluxo. Introduzimos aqui
um comprimento de mistura ( mixing length) 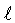 para representar a distância vertical média,
ou livre caminho médio, que o elemento
se move antes de se dissolver no meio circundante.
Ao mesmo tempo, elementos (bolhas) frias da camada superior
afundam uma distância
para representar a distância vertical média,
ou livre caminho médio, que o elemento
se move antes de se dissolver no meio circundante.
Ao mesmo tempo, elementos (bolhas) frias da camada superior
afundam uma distância
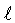 e se dissolvem. Este mesmo
efeito ocorre quando fervemos água em uma panela;
próximo à fervura, inicia-se um fluxo de matéria quente
do fundo para a superfície, e vice-versa.
Em termos
do comprimento de mistura, podemos representar a distância
média que um elemento se move em um momento arbitrário como:
Desta forma obtemos das equações (1.56) e (1.57):
e se dissolvem. Este mesmo
efeito ocorre quando fervemos água em uma panela;
próximo à fervura, inicia-se um fluxo de matéria quente
do fundo para a superfície, e vice-versa.
Em termos
do comprimento de mistura, podemos representar a distância
média que um elemento se move em um momento arbitrário como:
Desta forma obtemos das equações (1.56) e (1.57):
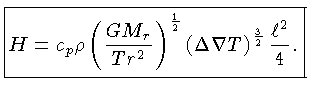 |
(1.58) |
A equação (1.58) representa nossa relação final entre
o fluxo de energia convectivo e o gradiente de temperatura.
Ela envolve uma grande incerteza, o valor do comprimento de
mistura.
Deve ficar claro que a teoria do comprimento
de mistura representa uma extrema simplificação
ao processo físico real de convecção,
pois é uma aproximação local, isto é,
assume que o fluxo é dado pelo valor local do gradiente
de temperatura e parâmetros termodinâmicos locais.
Experimentos em laboratório indicam que o comprimento
de mistura é geralmente comparável ao tamanho linear do
volume em que observamos convecção. Correspondentemente,
poderíamos igualar o comprimento de mistura à profundidade
da camada instável. Entretanto isto seria uma grande super-estimativa
do comprimento de mistura, para as camadas instáveis em que
a densidade decresce de um grande fator, da base até a
camada superior, como no caso em que a região convectiva
ocorre perto da superfície. Um valor mais próximo
da realidade é assumir que o comprimento de mistura 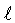 seja uma ou duas vezes a escala de variação de pressão,
isto é, a distância em que a pressão varia por um fator
seja uma ou duas vezes a escala de variação de pressão,
isto é, a distância em que a pressão varia por um fator 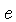 ,
,
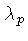 , definida como:
usando-se a equação do equilíbrio hidrostático (1.24),
e definindo
, definida como:
usando-se a equação do equilíbrio hidrostático (1.24),
e definindo 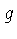 como a aceleração gravitacional.
Definimos
como a aceleração gravitacional.
Definimos
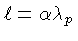 , onde
, onde 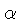 é chamado
do parâmetro do comprimento da mistura. Para
é chamado
do parâmetro do comprimento da mistura. Para 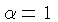 ,
denominamos a teoria de ML1. Uma variação é usar
esta relação somente se
,
denominamos a teoria de ML1. Uma variação é usar
esta relação somente se
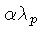 for menor
ou igual à distância da posição em questão até o
limite superior da zona de convecção. Se maior,
usamos esta última distância; esta aproximação chama-se ML2.
As observações recentes indicam também que o comprimento
de mistura não é o mesmo para tipos de estrelas diferentes,
e nem mesmo para profundidades diferentes da mesma estrela,
isto é, próximo ao núcleo ou próximo à superfície.
Para as estimativas seguintes, usaremos
Veremos que a incerteza neste valor é de pouca consequência
para zonas de convecção no núcleo de uma estrela. A
incerteza em
for menor
ou igual à distância da posição em questão até o
limite superior da zona de convecção. Se maior,
usamos esta última distância; esta aproximação chama-se ML2.
As observações recentes indicam também que o comprimento
de mistura não é o mesmo para tipos de estrelas diferentes,
e nem mesmo para profundidades diferentes da mesma estrela,
isto é, próximo ao núcleo ou próximo à superfície.
Para as estimativas seguintes, usaremos
Veremos que a incerteza neste valor é de pouca consequência
para zonas de convecção no núcleo de uma estrela. A
incerteza em 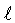 introduz, entretanto, incertezas significativas nos modelos,
quando a instabilidade convectiva ocorre logo abaixo
da fotosfera de uma estrela - como muitas vezes é o caso -
e portanto introduz incertezas significativas na estrutura
e extensão das camadas externas de um modelo estelar. De fato,
a falta de uma boa teoria hidrodinâmica de convecção
é um dos mais sérios problemas na compreensão
de modelos de interiores estelares. Isto se dá porque as
equações hidrodinâmicas, incluindo turbulência,
são altamente não locais e não lineares,
causando movimentos inomogêneos. Já existem
algumas aproximações calculadas,
por exemplo, os
modelos numéricos hidrodinâmicos bi e tri-dimensionais,
dependentes do tempo, de convecção compressível,
de Bernd
Freytag, (4.4 MB mpeg de Betelgeuse)
e as mostradas abaixo.
introduz, entretanto, incertezas significativas nos modelos,
quando a instabilidade convectiva ocorre logo abaixo
da fotosfera de uma estrela - como muitas vezes é o caso -
e portanto introduz incertezas significativas na estrutura
e extensão das camadas externas de um modelo estelar. De fato,
a falta de uma boa teoria hidrodinâmica de convecção
é um dos mais sérios problemas na compreensão
de modelos de interiores estelares. Isto se dá porque as
equações hidrodinâmicas, incluindo turbulência,
são altamente não locais e não lineares,
causando movimentos inomogêneos. Já existem
algumas aproximações calculadas,
por exemplo, os
modelos numéricos hidrodinâmicos bi e tri-dimensionais,
dependentes do tempo, de convecção compressível,
de Bernd
Freytag, (4.4 MB mpeg de Betelgeuse)
e as mostradas abaixo.
Para que a idade, tamanho e luminosidade do Sol calculados pelos
modelos sejam iguais às observadas, α=1.
Entretanto, Klaus Fuhrmann, M. Axer & Thomas Gehren
(1993, Astronomy & Astrophysics, 271, 451) demonstraram empiricamente que
as linhas de Balmer do espectro solar precisam
ser calculadas usando α=0,5.
Joachim Theurer,
Peter Ulmschneider (1938-)
& Wolfgang Kalkofen,
(1997, Astronomy & Astrophysics, 324, 717)
determinaram α=2,0 para explicar as
oscilações na atmosfera do Sol.
Francesco R. Ferraro, Elena Valenti, Oscar Straniero, &
Livia Origlia, em 2006 no
Astrophysical
Journal, 642, 225 determinaram α=2,17 para fitar
28 cúmulos globulares.
Hans-Günther Ludwig, Stefan Jordan & Matthias Steffen
(1994, Astronomy & Astrophysics, 284, 105)
mostraram que pode-se construir modelos uni-dimensionais
com a teoria de comprimento de mistura para anãs brancas
com
ML1/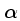 =1,5 equivalentes aos
modelos hidrodinâmicos. Entretanto um parâmetro maior
é necessário para representar a estratificação de temperatura
nas camadas na base da zona de convecção.
=1,5 equivalentes aos
modelos hidrodinâmicos. Entretanto um parâmetro maior
é necessário para representar a estratificação de temperatura
nas camadas na base da zona de convecção.

Pierre Bergeron
Para que os espectros das anãs brancas com
atmosfera de hidrogênio tanto no ótico quanto
no ultravioleta sejam representados pela mesma temperatura
efetiva, Pierre Bergeron, François Wesemael, Gilles Fontaine,
Rex A. Saffer & Nicole F. Allard (1995, Astrophysical Journal, 449, 258)
demonstraram que é necessário utilizar-se
ML2/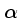 =0,6.
Para as anãs brancas com atmosfera de hélio, o melhor valor
é ML2/α=1.25, de acordo com
Alain Beauchamp, François Wesemael, Pierre Bergeron, Gilles Fontaine,
Rex A. Saffer, James Liebert & Pierre Brassard, 1999,
Astrophysical Journal, 516, 887.
Matthias Steffen, Hans Günther-Ludwig & Bernd Freytag
(1995, A&A, 300, 473) demonstraram que os modelos
unidimensionais para as anãs brancas não conseguem
fitar bem o espectro previsto pelos modelos hidrodinâmicos
para
=0,6.
Para as anãs brancas com atmosfera de hélio, o melhor valor
é ML2/α=1.25, de acordo com
Alain Beauchamp, François Wesemael, Pierre Bergeron, Gilles Fontaine,
Rex A. Saffer, James Liebert & Pierre Brassard, 1999,
Astrophysical Journal, 516, 887.
Matthias Steffen, Hans Günther-Ludwig & Bernd Freytag
(1995, A&A, 300, 473) demonstraram que os modelos
unidimensionais para as anãs brancas não conseguem
fitar bem o espectro previsto pelos modelos hidrodinâmicos
para
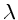 <1400Å.
<1400Å.
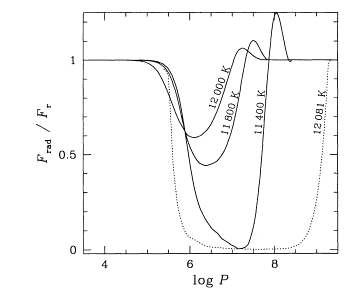 Comparação de modelos bi-dimensionais para a
zona de convecção superficial de uma anã branca DA, publicado
por Alfred Gautschy,
Hans Günther-Ludwig & Bernd Freytag (1996, Astronomy &
Astrophysics, 311, 493),
com um modelo
ML3=ML2/
Comparação de modelos bi-dimensionais para a
zona de convecção superficial de uma anã branca DA, publicado
por Alfred Gautschy,
Hans Günther-Ludwig & Bernd Freytag (1996, Astronomy &
Astrophysics, 311, 493),
com um modelo
ML3=ML2/ =2 (linha pontilhada).
As zonas de convecção dos modelos bidimensionais
se extendem até 10-15M* (para Tef=12600K) e
10-14M*
(para Tef=11 400K) são sempre menores
do que o ML3, que se extende até 8×10-15M*.
Note que o comprimento de mistura é um parâmetro livre. Nos modelos
de pulsação de anãs brancas, ele foi escolhido como ML3 para fitar
a temperatura da borda azul da faixa de instabilidade das DAVs,
mas este mesmo valor não fita os espectros observados.
Os fluxos acima de 1 indicam sobreimpulso (overshooting).
=2 (linha pontilhada).
As zonas de convecção dos modelos bidimensionais
se extendem até 10-15M* (para Tef=12600K) e
10-14M*
(para Tef=11 400K) são sempre menores
do que o ML3, que se extende até 8×10-15M*.
Note que o comprimento de mistura é um parâmetro livre. Nos modelos
de pulsação de anãs brancas, ele foi escolhido como ML3 para fitar
a temperatura da borda azul da faixa de instabilidade das DAVs,
mas este mesmo valor não fita os espectros observados.
Os fluxos acima de 1 indicam sobreimpulso (overshooting).
Pier-Emmanuel Tremblay, em sua tese de doutorado de 2011
propõe α=0,8 para as anãs brancas DAs, mas em seu artigo
de 2013, no
Astronomy &
Astrophysics, 552, 13, com Hans-Günter Ludwig, Matthias Steffen & Bernd Freytag,
demonstra que os cálculos tri-dimensionais (150×150×150 pontos) com o código
CO5BOLD são necessários para corrigir os valores tanto
de α=0,6 quanto de α=0,8.
O mesmo código também foi usado por Elisabetta Caffau, Hans-Günter Ludwig, Matthias Steffen para
estudar o Sol
e o efeito da granulação na determinação das abundâncias solares,
estudando 1,2 h de tempo solar, em uma caixa de 140×140×150,
representando 5,6×5,6×2,3 Mm3.
Ana Bonaca e colaboradores, em seu artigo de 2012 estudaram as pulsações das estrelas observadas
com o satélite Kepler e, como o raio do modelo é correlacionado
ao valor de α, concluíram que
o valor solar de α=2,12 não é adequado para todas as estrelas,
aumentando com a metalicidade da estrela, propondo
α=a + b log g+ c log Tef + d [Fe/H]
onde [Fe/H] é a metalicidade em relação ao Sol,
com a=7,97±0.27, b=-0,31±0,09, c=-1,33±0,80 e
d=0,48±0,12.
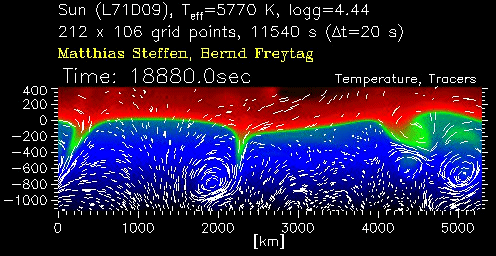 Simulação bi-dimensional da convecção solar,
mostrando as inomogeneidades
Simulação bi-dimensional da convecção solar,
mostrando as inomogeneidades
 Simulação tri-dimensional da convecção no núcleo de
uma estrela massiva.
Simulação tri-dimensional da convecção no núcleo de
uma estrela massiva.
 Vittorio M. Canuto & Italo Mazzitelli, em 1991,
(Stellar turbulent convection - A new model and applications,
Astrophysical Journal, 370, 295)
introduziram uma
teoria de convecção sem parâmetros livres, que leva em conta as
cerca de 109 escalas de mistura presentes na convecção.
Neste artigo eles propõem que o uso de MLT com o comprimento
de mistura igual à distância do ponto ao topo da camada de
convecção, isto é, sem o parâmetro
livre α
em
Vittorio M. Canuto & Italo Mazzitelli, em 1991,
(Stellar turbulent convection - A new model and applications,
Astrophysical Journal, 370, 295)
introduziram uma
teoria de convecção sem parâmetros livres, que leva em conta as
cerca de 109 escalas de mistura presentes na convecção.
Neste artigo eles propõem que o uso de MLT com o comprimento
de mistura igual à distância do ponto ao topo da camada de
convecção, isto é, sem o parâmetro
livre α
em
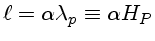 ,
é adequado, mas a expressão do fluxo convectivo precisa
ser modificada para incluir os diversos tamanhos de bolha,
aumentando o fluxo convectivo.
,
é adequado, mas a expressão do fluxo convectivo precisa
ser modificada para incluir os diversos tamanhos de bolha,
aumentando o fluxo convectivo.
A teoria que leva em conta todo o espectro de tamanhos das
bolhas foi ampliada por
Vittorio M. Canuto,
Itzhak Goldman
& Italo Mazzitelli, em 1996,
Turbulent Convection: Old and New Models,
(Astrophysical Journal, 467, 385).
No artigo
Selfconsistent model for turbulent convection:
helioseismology, ages of globular clusters, and white dwarfs blue edge,
[Pacific Rim Conference on Stellar Astrophysics, ASP Conference Series; Vol. 138; ed. Kwing Lam Chan; K. S. Cheng; and H. P. Singh (1998), p.123], eles
demonstram que o efeito do uso desta teoria reduz a idade dos
cúmulos globulares entre 1 a 2 Ganos, e reproduz melhor a temperatura
observada das borda azul da faixa de instabilidade das anãs brancas.
Richard B. Stothers & Chao-wen Chin, no artigo
Tests of two convection theories for red giant and
red supergiant envelopes (1995, Astrophysical Journal, 440, 297),
calculam modelos de 3 a 10 MSol com a teoria de
Canuto, Goldman & Mazzitelli e comparam a MLT. Os resultados são
similares, mas a MLT tem um parâmetro livre, o comprimento
de mistura.
Seguindo o desenvolvimento de François Roddier, no Progress in
Optics XIX (1981, ed. E. Wolf, North-Holland, p. 281),
o movimento de um fluido passa de laminar para
turbulento quando seu
número de Reynolds,
Re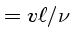 , excede um valor crítico
que depende da geometria do fluxo. Na definição do
número de Reynolds,
, excede um valor crítico
que depende da geometria do fluxo. Na definição do
número de Reynolds, 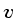 é a velocidade,
é a velocidade, 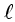 é o comprimento
característico do fluxo e
é o comprimento
característico do fluxo e 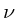 é a viscosidade cinemática.
No interior estelar, assim como na atmosfera da
Terra, os movimentos excedem este valor crítico
amplamente, de modo que o movimento convectivo é extremamente
turbulento.
No ar, a viscosidade cinemática
é da ordem de
é a viscosidade cinemática.
No interior estelar, assim como na atmosfera da
Terra, os movimentos excedem este valor crítico
amplamente, de modo que o movimento convectivo é extremamente
turbulento.
No ar, a viscosidade cinemática
é da ordem de
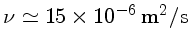 ,
,
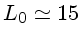 cm e
cm e 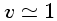 m/s, resultando um número
de Reynolds crítico da ordem de
Recrit
m/s, resultando um número
de Reynolds crítico da ordem de
Recrit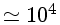 e qualquer escala maior terá
movimento turbulento.
e qualquer escala maior terá
movimento turbulento.
Em 1941,
Andrei Nikolaevich Kolmogorov (1903-1987)
(Doklady Akademii Nauk S.S.S.R, 30, 229) propôs que
em um meio turbulento, a energia cinética dos movimentos
de larga escala é transferida para movimentos com escalas
cada vez menores, até que este processo pare quando
a energia cinética for dissipada por fricção viscosa.
Num estado estacionário, a dissipação de energia
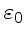 deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade
deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade 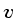 do movimento é proporcional
à escala
do movimento é proporcional
à escala 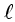 e à taxa de produção e
dissipação de energia
e à taxa de produção e
dissipação de energia
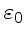 .
Como nas escalas maiores
.
Como nas escalas maiores
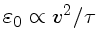 ,
onde
,
onde 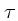 é o tempo característico
é o tempo característico
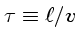 ,
,
Em uma análise espectral (de Fourier) da energia cinética em função
de um número de onda
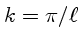 ,
a energia
,
a energia 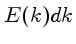 entre
entre 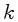 e
e 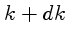 é proporcional a
é proporcional a 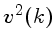 , logo
conhecida como a lei de Kolmogorov, que só é valida longe das bordas
, logo
conhecida como a lei de Kolmogorov, que só é valida longe das bordas
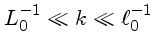 , onde
, onde 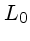 é a escala externa,
geralmente a escala da região que dá origem à turbulência,
e
é a escala externa,
geralmente a escala da região que dá origem à turbulência,
e 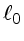 a escala na qual a dissipação por viscosidade ocorre.
A distribuição espectral de energia
a escala na qual a dissipação por viscosidade ocorre.
A distribuição espectral de energia 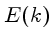 é definida
de modo que a energia cinética de turbulência por unidade
de massa seja:
O importante desta discussão é que a teoria de convecção altera a
estrutura dos modelos e sua composição química, modificando
o espectro observável por causa das dragagens que ocorrem
nos ramos gigantes e super-gigantes, trazendo material processado
para a atmosfera da estrela. Até mesmo a idade das estrelas dos
cúmulos são alteradas por modificações na forma de cálculo da
convecção.
é definida
de modo que a energia cinética de turbulência por unidade
de massa seja:
O importante desta discussão é que a teoria de convecção altera a
estrutura dos modelos e sua composição química, modificando
o espectro observável por causa das dragagens que ocorrem
nos ramos gigantes e super-gigantes, trazendo material processado
para a atmosfera da estrela. Até mesmo a idade das estrelas dos
cúmulos são alteradas por modificações na forma de cálculo da
convecção.





Próxima: Aproximação Adiabática para dT/dr
Volta: Transporte de Energia por Convecção
Anterior: Equilíbrio Convectivo
©
Modificada em 1 abril 2015
![]() , seu excesso
de temperatura será:
, seu excesso
de temperatura será:
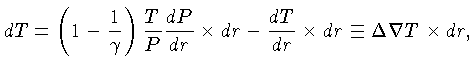
![]() precisa ser
determinada primeiro pela seguintes considerações
dinâmicas. A deficiência de densidade do elemento ascendente
sobre o meio circundante pode ser calculada, similarmente
ao excesso de temperatura, pela seguinte fórmula, usando-se
a desigualdade (1.52):
precisa ser
determinada primeiro pela seguintes considerações
dinâmicas. A deficiência de densidade do elemento ascendente
sobre o meio circundante pode ser calculada, similarmente
ao excesso de temperatura, pela seguinte fórmula, usando-se
a desigualdade (1.52):
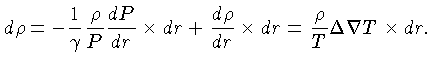
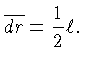
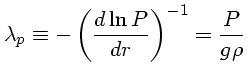
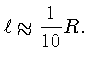
![]() =1,5 equivalentes aos
modelos hidrodinâmicos. Entretanto um parâmetro maior
é necessário para representar a estratificação de temperatura
nas camadas na base da zona de convecção.
=1,5 equivalentes aos
modelos hidrodinâmicos. Entretanto um parâmetro maior
é necessário para representar a estratificação de temperatura
nas camadas na base da zona de convecção.
 Pierre Bergeron
Pierre Bergeron
![$[{Fe/H}] = \log (\frac{N_{Fe}}{N_{H}})_{estrela}-\log (\frac{N_{Fe}}{N_{H}})_\odot$](feh.png)
 Vittorio M. Canuto & Italo Mazzitelli, em 1991,
(Stellar turbulent convection - A new model and applications,
Astrophysical Journal, 370, 295)
introduziram uma
teoria de convecção sem parâmetros livres, que leva em conta as
cerca de 109 escalas de mistura presentes na convecção.
Neste artigo eles propõem que o uso de MLT com o comprimento
de mistura igual à distância do ponto ao topo da camada de
convecção, isto é, sem o parâmetro
livre α
em
Vittorio M. Canuto & Italo Mazzitelli, em 1991,
(Stellar turbulent convection - A new model and applications,
Astrophysical Journal, 370, 295)
introduziram uma
teoria de convecção sem parâmetros livres, que leva em conta as
cerca de 109 escalas de mistura presentes na convecção.
Neste artigo eles propõem que o uso de MLT com o comprimento
de mistura igual à distância do ponto ao topo da camada de
convecção, isto é, sem o parâmetro
livre α
em
![]() ,
é adequado, mas a expressão do fluxo convectivo precisa
ser modificada para incluir os diversos tamanhos de bolha,
aumentando o fluxo convectivo.
,
é adequado, mas a expressão do fluxo convectivo precisa
ser modificada para incluir os diversos tamanhos de bolha,
aumentando o fluxo convectivo.
![]() , excede um valor crítico
que depende da geometria do fluxo. Na definição do
número de Reynolds,
, excede um valor crítico
que depende da geometria do fluxo. Na definição do
número de Reynolds, ![]() é a velocidade,
é a velocidade, ![]() é o comprimento
característico do fluxo e
é o comprimento
característico do fluxo e ![]() é a viscosidade cinemática.
No interior estelar, assim como na atmosfera da
Terra, os movimentos excedem este valor crítico
amplamente, de modo que o movimento convectivo é extremamente
turbulento.
No ar, a viscosidade cinemática
é da ordem de
é a viscosidade cinemática.
No interior estelar, assim como na atmosfera da
Terra, os movimentos excedem este valor crítico
amplamente, de modo que o movimento convectivo é extremamente
turbulento.
No ar, a viscosidade cinemática
é da ordem de
![]() ,
,
![]() cm e
cm e ![]() m/s, resultando um número
de Reynolds crítico da ordem de
Recrit
m/s, resultando um número
de Reynolds crítico da ordem de
Recrit![]() e qualquer escala maior terá
movimento turbulento.
e qualquer escala maior terá
movimento turbulento.
![]() deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade
deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade ![]() do movimento é proporcional
à escala
do movimento é proporcional
à escala ![]() e à taxa de produção e
dissipação de energia
e à taxa de produção e
dissipação de energia
![]() .
Como nas escalas maiores
.
Como nas escalas maiores
![]() ,
onde
,
onde ![]() é o tempo característico
é o tempo característico
![]() ,
,
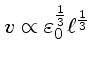
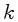 e
e 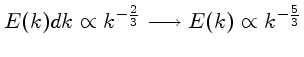
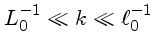 , onde
, onde