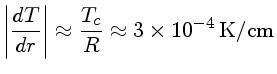Próxima: Características da Convecção no Interior Estelar Volta: Transporte de Energia por Convecção Anterior: Transporte de Energia por Convecção

Aproximação Adiabática para o Gradiente de Temperatura

Para obtermos uma relação completa entre o fluxo total de energia e o gradiente de temperatura, podemos escrever:

$$\boxed {H=H_{\rm radiativo} + H_{\rm convectivo}}$$ (1.59)

Se introduzirmos na equação (1.59) o fluxo radiativo dado pela equação (1.51) e para o fluxo convectivo o valor dado pela equação (1.58), podemos resolver a equação para o gradiente de temperatura. A solução é simplificada pela seguinte estimativa de ordem de grandeza. Vamos novamente estimar os valores para um ponto médio no Sol. Vamos também usar para o fluxo convectivo, seu limite superior, que é o fluxo total. Se introduzirmos estes valores na equação (1.58), obtemos para o excesso do gradiente de temperatura:

$\Delta\nabla T \approx 2 \times 10^{-10}{K/cm}$

Este valor deve ser comparado com o valor do gradiente, que pode ser estimado como:

$\vert\frac{dT}{dr}\vert \approx \frac{T_c}{R} \approx 3 \times 10^{-4}{K/cm}$

Vemos portanto que o excesso do gradiente verdadeiro sobre o gradiente adiabático é somente um milionésimo do gradiente de temperatura verdadeiro. Dentro de nossa precisão, é portanto totalmente permissível ignorar o excesso do gradiente de temperatura e, em uma zona convectiva, igualar o gradiente de temperatura ao gradiente adiabático. Desta forma, de acordo com a equação (1.55):

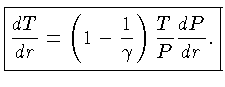$${\frac{dT}{dr}= \left(1 - \frac{1}{\gamma}\right)\frac{T}{P}\frac{dP}{dr}}$$ (1.60)

Somente próximo à fotosfera, onde a densidade e o comprimento de mistura são pequenos, a equação (1.60) não é uma boa aproximação. Neste caso, precisamos utilizar a equação (1.58) explicitamente, com sua incerteza em 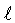$\ell$ desconfortável.

Próxima: Características da Convecção no Interior Estelar Volta: Transporte de Energia por Convecção Anterior: Transporte de Energia por Convecção