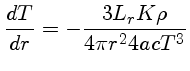Próxima: Overshooting e Semiconvecção
Volta: Transporte de Energia por Convecção
Anterior: Aproximação Adiabática para o Gradiente de
Com a ajuda de nossas estimativas numéricas anteriores, podemos
estimar o movimentos que ocorrem em uma zona convectiva no interior
estelar. Para o excesso de temperatura médio, ou
deficiência dentro de um elemento em movimento em relação
ao meio circundante, encontramos:
Esta é realmente uma flutuação pequena em comparação
com a temperatura média de vários milhões de graus. A velocidade
média do elemento em movimento pode ser calculada da
equação de energia cinética (1.57):
Novamente, as velocidades são muito baixas comparadas com as
velocidades térmicas, que são de centenas de km por segundo no
interior estelar
[vtérmicaH (T=10 milhões K)= 11 km/s].
Como as velocidades convectivas são muito
menores que as velocidades térmicas, por cerca de quatro ordens
de magnitude, os efeitos hidrodinâmicos dos movimentos
convectivos são cerca de oito ordens de magnitude
menores do que a pressão do gás.
A convecção é portanto subsônica, e a pressão
turbulenta menor do que a pressão total. Se as velocidades
convectivas se tornarem supersônicas, as hipóteses
básicas da teoria de mistura,
a aproximação considerada,
do francês Joseph Boussinesq (1842-1929), estão violadas.
A aproximação
Boussinesq em geral funciona bem em laboratório, onde a
escala de profundidade é comparável com a escala
do experimento, o que não é o caso nas estrelas.
Esta conclusão
é muito importante, porque justifica nossa
hipótese intrínseca de que os movimentos convectivos
não perturbam o equilíbrio hidrostático.
Podemos então calcular o tempo de vida médio de um
elemento de turbulência:
Este tempo é longo do ponto de vista de turbulência, mas
é extremamente curto comparado a escala de tempo de evolução
estelar. Desta maneira, a zona de convecção deve ser muito
bem misturada. Desta maneira, quando as reações nucleares
mudam a composição química nas partes mais quentes
de uma zona de convecção, estas mudanças são
aparentes, por mistura turbulenta, em todas as partes da
zona de convecção, em um tempo muito curto.
Para a convecção nas camadas externas do Sol, pode-se
obter
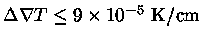 e
e
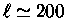 km, de modo que
km, de modo que
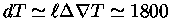 K.
K.
Um exemplo da existência da zona de convecção interior
pode ser obtido examinando-se uma estrela de população I,
isto é, do disco da nossa galáxia, com X=0,7 e Z=0,03,
e 30 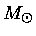 . Essa estrela terá uma temperatura
central de
. Essa estrela terá uma temperatura
central de
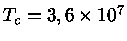 K, uma densidade central de
K, uma densidade central de
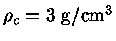 , luminosidade total de
, luminosidade total de
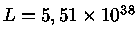 ergs/s
e raio
ergs/s
e raio
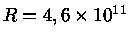 cm. Para manter essa luminosidade,
a estrela terá uma taxa de produção de energia central
de
cm. Para manter essa luminosidade,
a estrela terá uma taxa de produção de energia central
de
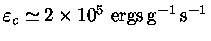 ,
e a opacidade será dominada por espalhamento de elétrons,
como veremos na próxima seção, com
,
e a opacidade será dominada por espalhamento de elétrons,
como veremos na próxima seção, com
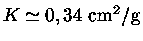 . A pressão total pode
ser calculada como
. A pressão total pode
ser calculada como
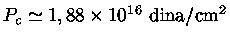 ,
incluindo-se a pressão de radiação, sendo que a pressão do
gás contribui com 77,5% da pressão total. Para essas
condições
,
incluindo-se a pressão de radiação, sendo que a pressão do
gás contribui com 77,5% da pressão total. Para essas
condições
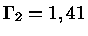 , logo
, logo
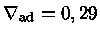 ,
e
,
e
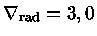 . Portanto
. Portanto
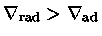 , comprovando que existe
uma zona de convecção central.
Podemos calcular, para essas condições,
, comprovando que existe
uma zona de convecção central.
Podemos calcular, para essas condições,
Se assumirmos, para simplificar, 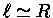 , e para a
gravidade
, e para a
gravidade
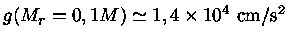 ,
obteremos
,
obteremos
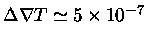 , e
, e
 ,
isto é, a convecção transporta 90% do fluxo total.
Na seqüência principal, as estrelas com
,
isto é, a convecção transporta 90% do fluxo total.
Na seqüência principal, as estrelas com
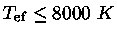 têm zona de convecção superficial eficiente.
têm zona de convecção superficial eficiente.
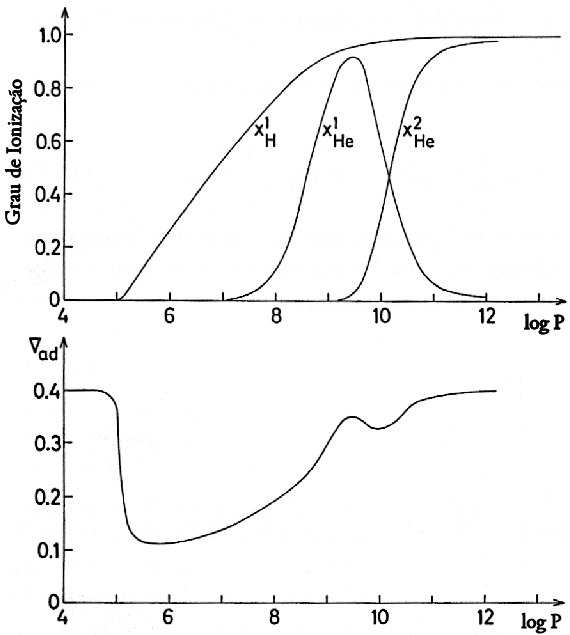
Ionização nas camadas externas do Sol e seu efeito do gradiente adiabático.
Sumarizando, os movimentos em uma zona de convecção são
turbulentos, mas tão lentos que não têm qualquer efeito
hidrodinâmico. Os movimentos convectivos são
altamente eficientes no transporte de energia devido ao alto
conteúdo em energia térmica dos gases no interior estelar.
A mistura turbulenta é tão rápida que as zonas convectivas
são praticamente homogêneas a todo tempo.
Do ponto de vista da construção de modelos estelares,
podemos extrair a seguinte receita. Em cada camada do modelo,
- calcule o gradiente de pressão da condição
de equilíbrio hidrostático (1.24),
e
- o gradiente de temperatura
da equação de equilíbrio radiativo (1.51).
- Introduza estes valores na
condição de estabilidade de Schwarzschild (1.53). Se a condição é satisfeita,
convecção não ocorre e o gradiente de temperatura
calculado pela equação de equilíbrio radiativo (1.51)
é o correto.
- Se a condição de
estabilidade de Schwarzschild (1.53) não
é satisfeita, convecção
ocorre e o gradiente calculado na equação de equilíbrio
radiativo (1.51) não pode ser usado.
Use o gradiente adiabático
dado pela equação (1.60), que tem precisão suficiente.
No artigo de 2015,
The Stagger-grid: A grid of 3D stellar atmosphere models
III. The relation to mixing length convection theory,
publicado no
Astronomy & Astrophysics, 573, A89,
Zazralt Magic, Achim Weiss e Martin Asplund
comparam resultados de 1-dimensão calculados com a teoria de comprimento de mistura (MLT) com modelos tri-dimensionais,
e obtém que modelos com αSol=1,98 na base da zona de convecção para o Sol são similares,
mas que α varia entre 1,7 e 2,4 para diferentes massas e temperaturas, decrescendo para temperaturas mais altas.
No arXiv:1503.00342,
Beyond mixing-length theory: A step toward 321D,
W. David Arnett, Casey Meakin,
Maxime Viallet,
Simon W. Campbell,
John Lattanzio &
Mirolslav Mocak,
apresentam algoritmos para substituir a MLT por algoritmos baseados na solução das equações de
tridimensionais e dependentes do tempo.
Derivamos portanto as condições de equilíbrio
necessárias para calcular modelos de interiores estelares.
As equações contém relações entre
pressão,
densidade e temperatura. Precisamos de uma equação
de estado para relacionar as três variáveis.
A opacidade
é um fator decisivo na equação de equilíbrio
radiativo; precisamos conhecer a opacidade em função
da temperatura e da densidade. A equação básica
de equilíbrio térmico requer o conhecimento das
taxas de produção de energia por reações nucleares
para as várias condições de temperatura e densidade.





Próxima: Overshooting e Semiconvecção
Volta: Transporte de Energia por Convecção
Anterior: Aproximação Adiabática para o Gradiente de
©
Modificada em 27 dez 2014
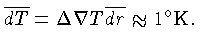
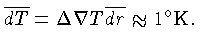
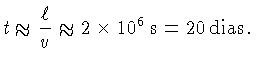
![]() e
e
![]() km, de modo que
km, de modo que
![]() K.
K.
![]() . Essa estrela terá uma temperatura
central de
. Essa estrela terá uma temperatura
central de
![]() K, uma densidade central de
K, uma densidade central de
![]() , luminosidade total de
, luminosidade total de
![]() ergs/s
e raio
ergs/s
e raio
![]() cm. Para manter essa luminosidade,
a estrela terá uma taxa de produção de energia central
de
cm. Para manter essa luminosidade,
a estrela terá uma taxa de produção de energia central
de
![]() ,
e a opacidade será dominada por espalhamento de elétrons,
como veremos na próxima seção, com
,
e a opacidade será dominada por espalhamento de elétrons,
como veremos na próxima seção, com
![]() . A pressão total pode
ser calculada como
. A pressão total pode
ser calculada como
![]() ,
incluindo-se a pressão de radiação, sendo que a pressão do
gás contribui com 77,5% da pressão total. Para essas
condições
,
incluindo-se a pressão de radiação, sendo que a pressão do
gás contribui com 77,5% da pressão total. Para essas
condições
![]() , logo
, logo
![]() ,
e
,
e
![]() . Portanto
. Portanto
![]() , comprovando que existe
uma zona de convecção central.
Podemos calcular, para essas condições,
, comprovando que existe
uma zona de convecção central.
Podemos calcular, para essas condições,