




Próxima: Binárias Próximas
Volta: Interiores Estelares
Anterior: Formação Estelar
Estrelas Binárias
Um grande número de estrelas está em sistemas binários e
múltiplos, e sua evolução depende não somente da massa da estrela
mas também da separação entre elas. Se as estrelas estão separadas
mais do que 10× o raio que terão quando supergigantes,
suas evoluções são como as de estrelas não binárias. Para distâncias
menores, existe interação entre as estrelas que afeta sua evolução.
Consideremos duas estrelas de massa
M1
e
M2
separadas por uma distância
a
orbitando o centro
de massa do sistema.
No sistema de referência em rotação com o sistema binário,
o movimento de uma partícula de massa
m
é dado pela
relação:
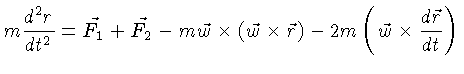 |
(1.126) |
onde 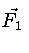 e
e 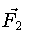 são as forças gravitacionais
sobre
m
causadas pelas estrelas de massas
são as forças gravitacionais
sobre
m
causadas pelas estrelas de massas 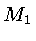 e
e 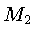 ,
e os dois últimos termos na equação (1.126)
representam a força centrífuga e a força de
Coriolis [Gustav-Gaspard Coriolis (1792-1843)].
A origem do sistema em rotação é o centro
de massa do sistema e
,
e os dois últimos termos na equação (1.126)
representam a força centrífuga e a força de
Coriolis [Gustav-Gaspard Coriolis (1792-1843)].
A origem do sistema em rotação é o centro
de massa do sistema e 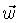 é a velocidade orbital
angular do sistema, apontando na direção do eixo z.
é a velocidade orbital
angular do sistema, apontando na direção do eixo z.
A força centrífuga pode ser derivada do potencial
Como a força de Coriolis é perpendicular à
direção de movimento, ela não pode realizar
trabalho sobre a massa pontual
m.
Se
m
está no plano (x,y), sua energia é dada por
e
O potencial V(x,y,0) tem máximos em três pontos críticos
que são chamados de pontos Lagrangianos no eixo x,
e dois no eixo y. Como são pontos de máximos,
podem ser
calculados calculando-se dV/dx=0 e dV/dy=0.
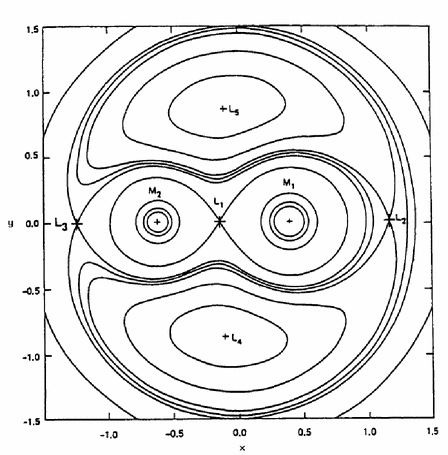 Equipotenciais de um sistema binário de massas similares,
mostrando os 5 pontos lagrangianos: L1 a L5. A equipotencial
que passa por L1 chama-se Lóbulo de Roche e, quando uma estrela
se expande até essa equipotencial, transfere massa para a companheira.
Equipotenciais de um sistema binário de massas similares,
mostrando os 5 pontos lagrangianos: L1 a L5. A equipotencial
que passa por L1 chama-se Lóbulo de Roche e, quando uma estrela
se expande até essa equipotencial, transfere massa para a companheira.
A teoria dos pontos Lagrangianos foi desenvolvida em
1772 pelo matemático francês
Joseph Louis Lagrange (1736-1813).
O ponto Lagrangiano
L1,
localizado no eixo x,
entre as duas estrelas, é de particular importância porque
se uma das estrelas se expande suficientemente tal que parte de
sua superfície atinge o ponto 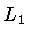 , ocorrerá transferência de
massa entre as estrelas. A curva equipotencial que inclui o ponto
, ocorrerá transferência de
massa entre as estrelas. A curva equipotencial que inclui o ponto
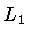 é chamada de lóbulo de Roche
[Edouard Roche (1820-1883)].
As equipotenciais próximas de
é chamada de lóbulo de Roche
[Edouard Roche (1820-1883)].
As equipotenciais próximas de 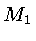 e
e 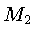 são quase
esféricas em torno das estrelas individuais, enquanto
que as equipotenciais externas ao lóbulo de Roche envolvem
as duas estrelas.
são quase
esféricas em torno das estrelas individuais, enquanto
que as equipotenciais externas ao lóbulo de Roche envolvem
as duas estrelas.
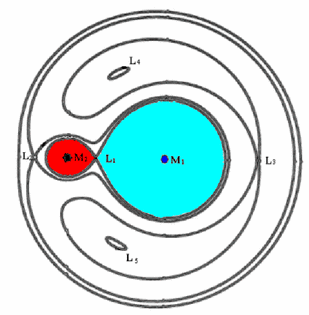 Equipotenciais de um sistema binário de massas diferentes.
Equipotenciais de um sistema binário de massas diferentes.





Próxima: Binárias Próximas
Volta: Interiores Estelares
Anterior: Formação Estelar
 Astronomia
e Astrofísica
Astronomia
e Astrofísica

©
Modificada em 19 Jun 2006
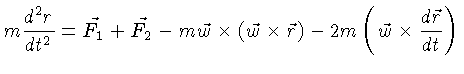
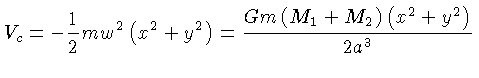
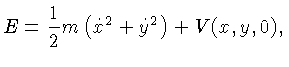
![$ - \frac{GmM_1}{[(x-x_1^2)^2+y^2]^{1/2}} - \frac{GmM_2}{[(x-x_2^2)^2+y^2]^{1/2}} -$](img966.gif)
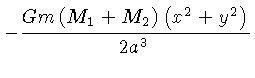


![]()