
 Foto da nuvem molecular Barnard 68 que está
a 500 anos-luz da Terra, na direção da constelação de
Ofiúco, 6,5×6,5′, com cerca de meio ano-luz de diâmetro e com uma temperatura de -263C e está
colapsando.
A foto da esquerda foi obtida com o telescópio de 8,2
do European Southern Observatory, no ótico.
À direita está a foto em cor falsa
obtida no telescópio
de 3,5m do European Southern
Observatory, composta de três exposições no infravermelho,
em 1,25, 1,65 e 2,16μm.
À direita, mosaico de fotos do Telescópio Espacial Hubble da Nuvem de Órion,
uma das regiões de formação estelar mais próxima de nós, com 65'x60'.
Tem uma extensão de aproximadamente 24 anos-luz e está a uma
distância de 1344±20 anos-luz.
Foto da nuvem molecular Barnard 68 que está
a 500 anos-luz da Terra, na direção da constelação de
Ofiúco, 6,5×6,5′, com cerca de meio ano-luz de diâmetro e com uma temperatura de -263C e está
colapsando.
A foto da esquerda foi obtida com o telescópio de 8,2
do European Southern Observatory, no ótico.
À direita está a foto em cor falsa
obtida no telescópio
de 3,5m do European Southern
Observatory, composta de três exposições no infravermelho,
em 1,25, 1,65 e 2,16μm.
À direita, mosaico de fotos do Telescópio Espacial Hubble da Nuvem de Órion,
uma das regiões de formação estelar mais próxima de nós, com 65'x60'.
Tem uma extensão de aproximadamente 24 anos-luz e está a uma
distância de 1344±20 anos-luz.
As observações indicam que as estrelas nascem da matéria
interestelar, provavelmente quando uma nuvem de gás se torna
gravitacionalmente instável, possivelmente pela passagem
de uma onda de choque causada pela explosão de uma supernova
nas proximidades, ou pela passagem de uma onda de densidade,
como aquelas teoricamente responsáveis pelos braços
espiras das galáxias, e
colapsa. A existência de nuvens
moleculares densas, como a Nuvem de Órion,
onde existem muitas estrelas jovens, dos glóbulos de Bok
[Bart Jan Bok (1906-1983)],
com sua emissão principalmente no infra-vermelho, dos envoltórios
das estrelas T Tauri, que são estrelas recém formadas,
todos corroboram a idéia da relação entre nuvens
de gás e a formação de estrelas.
Na nossa galáxia, as nuvens moleculares gigantes chegam a
6 milhões de massas solares
(Jonathan P. Williams, Leo Blitz, Christopher F. McKee,
2000, The Structure and Evolution of Molecular Clouds: from Clumps to Cores to the IMF". Protostars and Planets IV).
 Glóbulos de Bok absorvendo luz no centro da
nebulosa de emissão e região de formação
estelar NGC 281. Imagem obtida com a
Advanced Camera for Surveys do Telescópio Espacial Hubble
em outubro de 2005. A nebulosa está localizada a 9500 anos-luz de
nós, na direção da constelação da
Cassiopéia.
Glóbulos de Bok absorvendo luz no centro da
nebulosa de emissão e região de formação
estelar NGC 281. Imagem obtida com a
Advanced Camera for Surveys do Telescópio Espacial Hubble
em outubro de 2005. A nebulosa está localizada a 9500 anos-luz de
nós, na direção da constelação da
Cassiopéia.
Na Via Láctea há aproximadamente 2 a 4 × bilhões de massas solares
em gás molecular e uma quantidade similar de hidrogênio e
aproximadamente 3 massas solares por ano são transformadas em estrelas.
Como somente cerca de 2% da massa de uma nuvem molecular tipicamente
é convertida em estrelas, cerca de 150 massas solares por ano de gás
por ano se transforma em nuvens moleculares formadoras de estrelas.
As nuvens moleculares são condensações no gás atômico largamente distribuído
pela galáxia. Estas condensações só sobrevivem por cerca de 107
anos, e estão constantemente sendo formadas e destruídas.
As propriedades médias da região central das nuvens moleculares
são:
- Densidade média
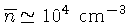 ,
consistindo principalmente de hidrogênio molecular
,
consistindo principalmente de hidrogênio molecular
- Temperatura média
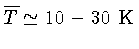
- Campo magnético médio
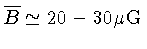
- Razão de gás ionizado (por raios cósmicos) para gás neutro
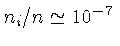
- Tamanho
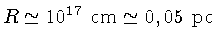
- Velocidade angular de rotação
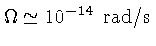
enquanto que as propriedades das estrelas, por exemplo o Sol, são:
- Densidade média
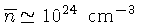 ,
consistindo principalmente de hidrogênio ionizado
,
consistindo principalmente de hidrogênio ionizado
- Temperatura média
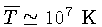
- Campo magnético médio na atmosfera
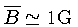
- Razão de gás ionizado para gás neutro
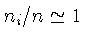 , exceto na atmosfera.
, exceto na atmosfera.
- Tamanho
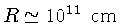
- Velocidade angular de rotação
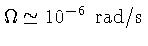
Portanto, para que haja a formação de uma estrela a partir da
nuvem, é necessário uma contração de um fator
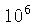 em raio, e
em raio, e 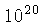 em densidade, o que causa dois
problemas imediatos:
em densidade, o que causa dois
problemas imediatos:
- Problema do Momentum Angular de Rotação:
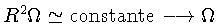 aumenta por
aumenta por
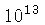
- Problema do Fluxo Magnético:
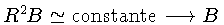 aumenta por
aumenta por
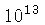
 e portanto a formação estelar tem que se dar com a
formação de um disco de acresção; a viscosidade
no disco permite
a acresção de massa ao centro, enquanto parte da massa é
acelerada para as partes externas, pela conservação
do momentum angular; ao mesmo tempo,
o disco é truncado no centro pelo
campo magnético, e matéria ionizada
tem que ser expelida por ejeção magneto-centrífuga,
possivelmente na forma de jatos bipolares,
por conservação do campo magnético,
como na imagem ao lado do objeto Herbig-Haro 30
[George Howard Herbig (1920-2013)
(1950, Astrophysical
Journal, 111, 11)
e Guillermo Haro (1913-1988) (1952, Astrophysical Journal, 115, 572)],
obtida com o Telescópio Espacial Hubble.
As nebulosas Herbig-Haro correspondem aos jatos colimados,
e suas (proto) estrelas têm discos circum-estelares e
são mais jovens que 100 milhões de anos.
e portanto a formação estelar tem que se dar com a
formação de um disco de acresção; a viscosidade
no disco permite
a acresção de massa ao centro, enquanto parte da massa é
acelerada para as partes externas, pela conservação
do momentum angular; ao mesmo tempo,
o disco é truncado no centro pelo
campo magnético, e matéria ionizada
tem que ser expelida por ejeção magneto-centrífuga,
possivelmente na forma de jatos bipolares,
por conservação do campo magnético,
como na imagem ao lado do objeto Herbig-Haro 30
[George Howard Herbig (1920-2013)
(1950, Astrophysical
Journal, 111, 11)
e Guillermo Haro (1913-1988) (1952, Astrophysical Journal, 115, 572)],
obtida com o Telescópio Espacial Hubble.
As nebulosas Herbig-Haro correspondem aos jatos colimados,
e suas (proto) estrelas têm discos circum-estelares e
são mais jovens que 100 milhões de anos.
Richard B. Larson
(2002, Monthly Notices of the Royal Astronomical
Society, 332, 155)
demonstra que as interações por força de maré entre os fragmentos
que se formam são possivelmente a maneira mais eficiente de
possibilitar a transferência do excesso de momentum angular
e permitir o colapso.
A fração de binárias aumenta com a massa das estrelas
(Hans Zinnecker & Harold W. Yorke, 2007, Annual Review of Astronomy & Astrophysics, 45, 481),
alcançando 70% para estrelas tipo O
(Hugues Sana et al. 2012,
Binary interaction dominates the evolution of massive stars,
Science 337, 444).
Como primeiro passo no cálculo, vamos derivar
o critério de Jeans, calculado em 1902 por
Sir James Hopwood Jeans (1877-1946),
calculando o colapso gravitacional ignorando tanto o
campo magnético quanto a rotação
(Philosophical Transactions of the Royal Society, Série A, 199,1).
Consideremos um gás homogêneo e infinito em repouso,
com densidade e temperatura constante em todos os pontos.
Primeiro, precisamos reconhecer que esta afirmação
é inconsistente, pois por razões de simetria, o
potencial gravitacional 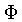 também deve ser constante,
mas a equação de Poisson [Siméon Denis Poisson (1781-1840)]:
também deve ser constante,
mas a equação de Poisson [Siméon Denis Poisson (1781-1840)]:
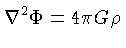 |
(1.106) |
demandaria que a densidade fosse nula (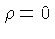 ).
Mesmo reconhecendo a inconsistência, definimos um meio
de densidade constante não nula, pois estamos interessados
em pequenas perturbações em uma esfera isotérmica
em equilíbrio hidrostático, que é um
estado inicial consistente.
).
Mesmo reconhecendo a inconsistência, definimos um meio
de densidade constante não nula, pois estamos interessados
em pequenas perturbações em uma esfera isotérmica
em equilíbrio hidrostático, que é um
estado inicial consistente.
O gás deve obedecer, além
da equação de Poisson (1.106), à equação hidrodinâmica
do movimento de Euler [Leonhard Euler (1707-1783)]:
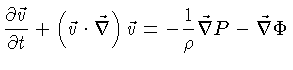 |
(1.107) |
à equação da continuidade
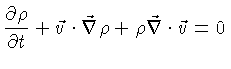 |
(1.108) |
e finalmente à equação do gás ideal
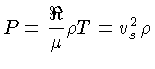 |
(1.109) |
onde 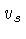 é a velocidade do som. Para o estado de equilíbrio,
assumimos
é a velocidade do som. Para o estado de equilíbrio,
assumimos
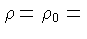 constante,
constante,
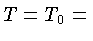 constante, e
constante, e 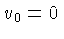 . O potencial gravitacional
de equilíbrio
. O potencial gravitacional
de equilíbrio 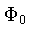 pode ser encontrado usando
a equação de Poisson
pode ser encontrado usando
a equação de Poisson
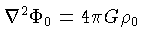 ,
e as condições de contorno no infinito.
,
e as condições de contorno no infinito.
Perturbamos agora o equilíbrio
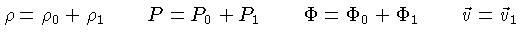 |
(1.110) |
onde as funções com subscrito 1 dependem do espaço
o do tempo, e já usamos 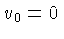 . Substituindo 1.110
em 1.106, 1.107, 1.108 e 1.109,
e assumindo que as perturbações são isotérmicas,
isto é, que a velocidade do som não é perturbada,
obtemos as seguintes relações em primeira ordem:
. Substituindo 1.110
em 1.106, 1.107, 1.108 e 1.109,
e assumindo que as perturbações são isotérmicas,
isto é, que a velocidade do som não é perturbada,
obtemos as seguintes relações em primeira ordem:
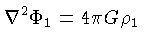 |
(1.111) |
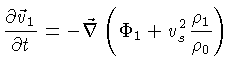 |
(1.112) |
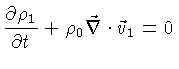 |
(1.113) |
Este é um sistema de equações diferenciais lineares e homogêneo,
com coeficientes constantes.
Sem perda de generalidade, podemos considerar perturbações
que se propagam apenas em uma dada direção, por exemplo 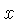 .
Podemos portanto assumir que existem
soluções proporcionais a
.
Podemos portanto assumir que existem
soluções proporcionais a
![$ \exp[i(kx+wt)]$](img899.gif) , de modo que
e definindo
, de modo que
e definindo
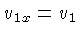 ,
,
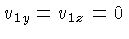 , obtemos:
, obtemos:
Este conjunto de equações terá solução não nula
se o determinante
é nulo.
Lembramos que se A é a matrix
Obtemos portanto a relação de dispersão:
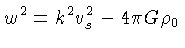 |
(1.117) |
Para números de onda 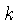 suficientemente grandes, o lado
direito da relação de dispersão (1.117)
é positivo, e
suficientemente grandes, o lado
direito da relação de dispersão (1.117)
é positivo, e 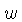 é real, e as perturbações
variam periodicamente no tempo. Como a amplitude não aumenta,
o equilíbrio é estável em relação a estas
perturbações de número de onda grande. Neste caso
não há colapso da nuvem.
é real, e as perturbações
variam periodicamente no tempo. Como a amplitude não aumenta,
o equilíbrio é estável em relação a estas
perturbações de número de onda grande. Neste caso
não há colapso da nuvem.
No limite
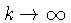 , a relação de dispersão
(1.117) resulta em
, a relação de dispersão
(1.117) resulta em
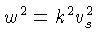 , que corresponde a ondas de som isotérmicas.
Neste caso, a gravidade não é importante, e qualquer compressão
é restaurada pelo aumento de pressão, com a perturbação
viajando pelo meio com a velocidade do som. Este caso novamente não leva à
formação estelar.
, que corresponde a ondas de som isotérmicas.
Neste caso, a gravidade não é importante, e qualquer compressão
é restaurada pelo aumento de pressão, com a perturbação
viajando pelo meio com a velocidade do som. Este caso novamente não leva à
formação estelar.
O caso que leva ao colapso da nuvem é quando
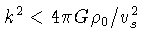 , o autovalor
, o autovalor 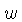 é da
forma
é da
forma
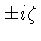 , onde
, onde 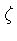 é real, já que definimos soluções proporcionais a exp[i(kx+wt)]. Portanto
existem perturbações proporcionais a
é real, já que definimos soluções proporcionais a exp[i(kx+wt)]. Portanto
existem perturbações proporcionais a
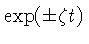 que crescem exponencialmente com o tempo, de modo
que não há equilíbrio, e a nuvem colapsa.
Definimos portanto um
número de onda característico
que crescem exponencialmente com o tempo, de modo
que não há equilíbrio, e a nuvem colapsa.
Definimos portanto um
número de onda característico
e o chamado
comprimento de onda de Jeans
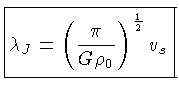 |
(1.118) |
de modo que quando
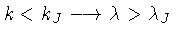 as perturbações são instáveis e a nuvem colapsa.
as perturbações são instáveis e a nuvem colapsa.
A condição de instabilidade
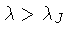 é chamada de critério de Jeans.
Para escalas maiores do que o comprimento de Jeans, a gravidade
sobrepassa a pressão, e a nuvem colapsa.
é chamada de critério de Jeans.
Para escalas maiores do que o comprimento de Jeans, a gravidade
sobrepassa a pressão, e a nuvem colapsa.
Para uma equação de gás ideal (1.109),
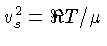 , e o comprimento de Jeans (1.118) se torna
, e o comprimento de Jeans (1.118) se torna
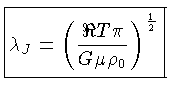 |
(1.119) |
A este comprimento de onda de Jeans, corresponde uma massa
de Jeans
onde escrevemos
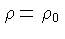 . Note que
. Note que 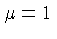 ,
,
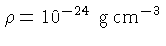 e
e 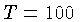 K são
as condições típicas das nuvens interestelares
de hidrogênio neutro. Desta forma, obtemos que somente
massas grandes,
K são
as condições típicas das nuvens interestelares
de hidrogênio neutro. Desta forma, obtemos que somente
massas grandes,
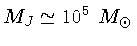 , podem colapsar
pela instabilidade de Jeans.
, podem colapsar
pela instabilidade de Jeans.
Uma derivação muito mais simplística, com o mesmo resultado, é considerar que quando
o tempo de queda livre é menor do que o tempo de cruzamento
do som, a gravidade é maior do que a pressão do gás e há colapso.
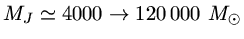
para
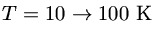
Se o colapso for isotérmico (nuvem transparente, não esquenta):
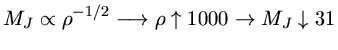
e ocorre fragmentação
Para densidades da ordem de
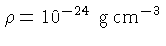 ,
o tempo de queda livre
,
o tempo de queda livre
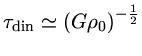 é da ordem de
é da ordem de 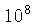 anos.
anos.
Primeiro a formação de
hidrogênio molecular - e depois a emissão de radiação infravermelha
oriunda da colisão do hidrogênio molecular com átomos de hidrogênio -
faz com que a temperatura nas partes mais densas caia para 200 a 300K.
Este é o momento da separação da matéria escura e da matéria comum.
Como as partículas de matéria escura não emitem radiação, elas
não se condensam e permanecem espalhadas na nuvem primordial.
Nas estrelas de população I e II,
os grãos de poeira e moléculas com elementos pesados resfriam as
nuvens com eficiência, até temperaturas de cerca de 10K.
Mas nas estrelas de população III este resfriamento por moléculas
pesadas e poeira não ocorre. Como a massa de Jeans (1.122) é
proporcional à temperatura elevada a 3/2 e inversamente proporcional
à raiz quadrada da sua pressão, as primeiras nuvens formadoras de
estrelas tiveram massa de Jeans quase 1000 vezes maior do que as atuais.
Acredita-se que as estrelas se formem por fragmentação
da nuvem colapsante, com os fragmentos tornando-se instáveis
após o início do colapso da nuvem, e colapsando mais
rápido do que a nuvem como um todo.
Mas será que a fragmentação continua até corpos
como planetas?
Se a nuvem colapsar isotermicamente,
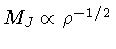 . Entretanto, se
o colapso for adiabático, isto é, sem perda de energia,
. Entretanto, se
o colapso for adiabático, isto é, sem perda de energia,
e a massa de Jean
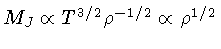 , isto é,
a massa de Jeans aumenta durante um colapso adiabático,
e a fragmentação não ocorre. A fragmentação
portanto só ocorre se o colapso for aproximadamente
isotérmico, isto é, se a nuvem irradiar a energia
gravitacional do colapso.
, isto é,
a massa de Jeans aumenta durante um colapso adiabático,
e a fragmentação não ocorre. A fragmentação
portanto só ocorre se o colapso for aproximadamente
isotérmico, isto é, se a nuvem irradiar a energia
gravitacional do colapso.
Portanto, se colapso adiabático (nuvem opaca):
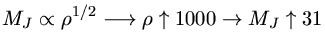
e não ocorre fragmentação
O astrônomo
inglês Sir Martin John Rees (1942-) publicou em 1976, no
Monthly Notices of the Royal Astronomical Society,
176, 483, uma demonstração de que a fragmentação
de nuvens
moleculares ocorre até uma massa mínima da ordem de 0,03 MSol,
estudando o colapso aproximadamente,
sem levar em conta os detalhes de como a energia é irradiada durante
o colapso. Veremos a seguir uma derivação simplística.
A menor anã marrom não binária encontrada nas Pleiades tem massa de
0,05 MSol,
de acordo com Martin R. Cossburn, Simon T. Hodgkin, Richard F. Jameson e David J. Pinfield
no artigo Discovery of the lowest mass brown dwarf in the Pleiades,
publicado em 1997 no Monthly Notices of the Royal Astronomical Society, 288, p. 23.
Gilles Chabrier
(2002), no artigo The Galactic Disk Mass Budget. II. Brown Dwarf Mass Function and Density, publicado em 2002 no Astrophysical Journal, 567, p. 304, estima que a
densidade de massa das anãs marrons corresponde a aproximadamente 10% da densidade
de massa das estrelas na nossa Galáxia.
As estrelas com massa inicial abaixo de 0,08 MSol tornam-se degeneradas
antes do início da ignição do hidrogênio e, portanto, nunca queimam o hidrogênio.
Para as estrelas com massa maior do que 13 MJúpiter, os elementos
frágeis D e Li são destruídos. Abaixo de 13 MJúpiter nenhuma reação
nuclear ocorre. Lembre-se que MJúpiter
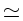 (1/1000)MSol.
(1/1000)MSol.
O tempo característico de queda livre do fragmento
é
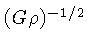 e a energia total a ser irradiada é
da ordem da energia gravitacional
e a energia total a ser irradiada é
da ordem da energia gravitacional
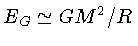 (ver Reserva de Energia de uma Estrela), onde
(ver Reserva de Energia de uma Estrela), onde 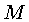 e
e 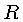 são a
massa e o raio do fragmento.
A quantidade de energia por unidade de tempo a ser irradiada para manter o
fragmento com a mesma temperatura é da ordem de
são a
massa e o raio do fragmento.
A quantidade de energia por unidade de tempo a ser irradiada para manter o
fragmento com a mesma temperatura é da ordem de
Entretanto, um fragmento de temperatura 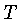 não pode irradiar mais do que um corpo negro com a mesma temperatura.
Se definirmos
não pode irradiar mais do que um corpo negro com a mesma temperatura.
Se definirmos 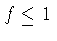 como o fator que leva em conta
que o fragmento irradia menos do que um corpo negro,
a taxa de perda de energia do fragmento é dada por:
onde
como o fator que leva em conta
que o fragmento irradia menos do que um corpo negro,
a taxa de perda de energia do fragmento é dada por:
onde 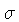 é a constante de Stefan-Boltzmann.
A transição de colapso isotérmico para adiabático
ocorre quando
é a constante de Stefan-Boltzmann.
A transição de colapso isotérmico para adiabático
ocorre quando 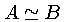 , isto é, quando
, isto é, quando
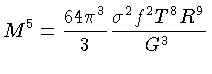 |
(1.123) |
Assumindo que a fragmentação termina quando a massa de
Jeans é igual a esta massa, substituimos 1.122
em 1.123,
e R por
obtendo a massa de Jeans no final da fragmentação:
para 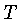 em K e usando
em K e usando
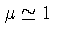 .
.
Para
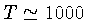 K e
K e
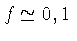 , obtemos
, obtemos
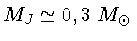 ,
ou seja, a fragmentação termina para fragmentos um
pouco menores que a massa solar.
As observações indicam que a
Função Inicial de Massa (IMF) dada pela
relação de Salpeter
[Edwin Ernest Salpeter (1925-2008)]
,
ou seja, a fragmentação termina para fragmentos um
pouco menores que a massa solar.
As observações indicam que a
Função Inicial de Massa (IMF) dada pela
relação de Salpeter
[Edwin Ernest Salpeter (1925-2008)]
é basicamente a mesma nas diversas regiões de nossa Galáxia e mesmo
nas galáxias próximas,
até z=2, equivalente a 7 Ganos
em relação ao tempo atual. A composição química do gás
parece ser similar à da Via Láctea para a mesma idade
(Bernard Ephraim Julius Pagel (1930-2007)
& Grazina Tautvaisiené, 1995, Monthly Notices
of the Royal Astronomical Society, 276, 505),
exceto para galáxias anãs.
Esfriamento
 O esfriamento das nuvens interestelares se dá principalmente
através da excitação colisional dos metais para níveis
proibidos, isto é, que se desexcitam principalmente por
emissão de fótons. Estes fótons têm níveis
de energia que não podem ser absorvidos normalmente,
e a energia é perdida da nuvem. Nas regiões HII as linhas
de O2+ dominam,
no gás neutro as linhas de
C+
e
Fe+,
e no gás molecular as linhas de
H2.
A formação de moléculas torna o gás mais denso porque o número
de partículas é reduzido.
Mas a formação de
H2
se dá principalmente por
catalização de grãos de poeira, produzidos pelas
estrelas de População I e II e retornados ao meio interestelar
por ventos e explosões.
Quanto mais metálico o gás, mais rápido ele esfria.
Sem metais (Pop. III) a fragmentação não ocorre porque o esfriamento é pequeno,
e a contração adiabática
(Richard B. Larson).
Raffaella Schneider, Kazuyuki Omukai, Simone Bianchi & Rosa Valiante
publicaram no Monthly Notices of the Royal Astronomical
Society, de 28 out 2011 uma estimativa de que
a fragmentação abaixo de 10 massas solares só ocorre
quando a quantidade de grãos de poeira excede 2,6-6,3×10-9
da quantidade de gás.
O esfriamento das nuvens interestelares se dá principalmente
através da excitação colisional dos metais para níveis
proibidos, isto é, que se desexcitam principalmente por
emissão de fótons. Estes fótons têm níveis
de energia que não podem ser absorvidos normalmente,
e a energia é perdida da nuvem. Nas regiões HII as linhas
de O2+ dominam,
no gás neutro as linhas de
C+
e
Fe+,
e no gás molecular as linhas de
H2.
A formação de moléculas torna o gás mais denso porque o número
de partículas é reduzido.
Mas a formação de
H2
se dá principalmente por
catalização de grãos de poeira, produzidos pelas
estrelas de População I e II e retornados ao meio interestelar
por ventos e explosões.
Quanto mais metálico o gás, mais rápido ele esfria.
Sem metais (Pop. III) a fragmentação não ocorre porque o esfriamento é pequeno,
e a contração adiabática
(Richard B. Larson).
Raffaella Schneider, Kazuyuki Omukai, Simone Bianchi & Rosa Valiante
publicaram no Monthly Notices of the Royal Astronomical
Society, de 28 out 2011 uma estimativa de que
a fragmentação abaixo de 10 massas solares só ocorre
quando a quantidade de grãos de poeira excede 2,6-6,3×10-9
da quantidade de gás.
As simulações de colapso de
Thomas H. Greif, Volker Springel, Simon D. M. White, Simon C.O. Glover, Paul C. Clark, Rowan J. Smith, Ralf S. Klessen & Volker Bromm, publicadas em
2011 no Astrophysical Journal, 737, 75, entretanto, propõem que a
fragmentação é recursiva e pode chegar até uma massa solar mesmo na Pop. III.

Imagem da estrela jovem, tipo T Tauri, HL Tau, e da nuvem molecular
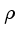
Ophiuchi.
As estrelas T Tauri foram descobertas em 1945, têm mais lítio que o Sol
no espectro, indicando que o núcleo ainda não atingiu
1 milhão K, têm linhas cromosféricas, são variáveis irregulares,
e mais da metade têm disco, observados pelo excesso de infra-vermelho
e emissão milimétrica.
A formação estelar ocorre nas nuvens moleculares massivas e densas
encontradas próximas ao plano da nossa Galáxia. A nebulosa do Saco de Carvão,
localizado a aproximadamente 150 pc na direção próxima ao Cruzeiro do Sul,
é um exemplo de uma nebulosa
escura. A região de 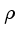 Ophiuchi,
altamente obscurecida, é
provavelmente a nuvem molecular e região de formação estelar
mais próxima (500 anos-luz). No ótico tem um raio de cerca de 5 pc e contêm
várias regiões HII.
Ophiuchi,
altamente obscurecida, é
provavelmente a nuvem molecular e região de formação estelar
mais próxima (500 anos-luz). No ótico tem um raio de cerca de 5 pc e contêm
várias regiões HII.
 Outra nuvem molecular é Sagittarius B-2
(Imagem composta
IR e submilimétrico
do centro da Galáxia e Sag B-2, do ESO/NASA)
localizada cerca de 200 pc do centro de nossa Galáxia e com uma
massa estimada em 3-10 milhões de massas solares,
uma das maiores nuvens moleculares da Via Láctea. Como a
extinção visual é de cerca de 25 magnitudes, esta
região só pode ser observada no rádio e infra-vermelho.
A molécula de CO é particularmente importante no estudo das
nuvens moleculares porque pode ser observada em 6 cm e
acredita-se que a razão CO/H2=10-4
seja a mesma em todas nuvens moleculares. Por dificuldades
instrumentais, a molécula
H2 só foi observada próximo do Sol, no
ultravioleta e no infra-vermelho, enquanto a molécula de
CO foi mapeada por toda a Via Láctea e mesmo em
galáxias próximas.
Outra nuvem molecular é Sagittarius B-2
(Imagem composta
IR e submilimétrico
do centro da Galáxia e Sag B-2, do ESO/NASA)
localizada cerca de 200 pc do centro de nossa Galáxia e com uma
massa estimada em 3-10 milhões de massas solares,
uma das maiores nuvens moleculares da Via Láctea. Como a
extinção visual é de cerca de 25 magnitudes, esta
região só pode ser observada no rádio e infra-vermelho.
A molécula de CO é particularmente importante no estudo das
nuvens moleculares porque pode ser observada em 6 cm e
acredita-se que a razão CO/H2=10-4
seja a mesma em todas nuvens moleculares. Por dificuldades
instrumentais, a molécula
H2 só foi observada próximo do Sol, no
ultravioleta e no infra-vermelho, enquanto a molécula de
CO foi mapeada por toda a Via Láctea e mesmo em
galáxias próximas.
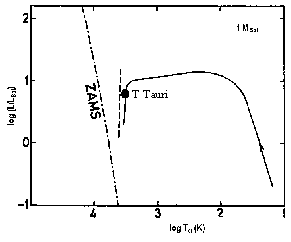
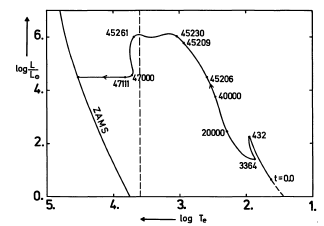
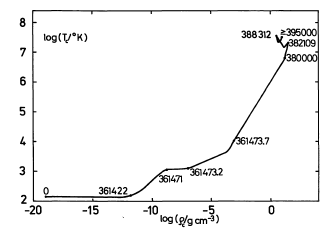 Diagrama Hertzsprung-Russel com o caminho evolucionário
para proto-estrelas de 1 e 60 massa solares. Os caminhos
começam no canto inferior direito, onde a radiação
emitida pelas nuvens é no infravermelho e, finalmente,
aproximam-se da seqüência principal de idade zero (ZAMS),
quando a proto-estrela finalmente atinge o equilíbrio
térmico e hidrostático. A proto-estrela de 60 MSol
ejeta parte do envelope, chegando à seqüência principal
com 17 MSol.
Os números indicam a idade da proto-estrela, em anos.
A linha tracejada indica o limite de
Hayashi (Immo Appenzeller e Walther M. Tscharnuter, 1974,
Astronomy & Astrophysics, 30, 423).
Diagrama Hertzsprung-Russel com o caminho evolucionário
para proto-estrelas de 1 e 60 massa solares. Os caminhos
começam no canto inferior direito, onde a radiação
emitida pelas nuvens é no infravermelho e, finalmente,
aproximam-se da seqüência principal de idade zero (ZAMS),
quando a proto-estrela finalmente atinge o equilíbrio
térmico e hidrostático. A proto-estrela de 60 MSol
ejeta parte do envelope, chegando à seqüência principal
com 17 MSol.
Os números indicam a idade da proto-estrela, em anos.
A linha tracejada indica o limite de
Hayashi (Immo Appenzeller e Walther M. Tscharnuter, 1974,
Astronomy & Astrophysics, 30, 423).
Quando a metalicidade aumenta, a posição da sequência principal
se move para temperaturas e luminosidades mais baixas, porque
as atmosferas de estrelas mais metálicas são mais opacas e,
portanto, mais vermelhas. E estrelas menos metálicas são mais
luminosas porque suas atmosferas são mais transparentes.
Richard B.
Larson publicou em 1969, no Monthly
Notices of the Royal Astronomical Society, 145, 271, cálculos
do colapso de uma nuvem originalmente homogênea com uma massa
solar.
- Na fase inicial, a nuvem colapsante é oticamente
fina (transparente) e aproximadamente isotérmica, com
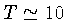 K.
K.
- Durante o colapso, a densidade central aumenta rapidamente,
a temperatura se mantém baixa pela emissão térmica dos grãos
de poeira, nas nuvens de população I e II,
enquanto a densidade nas partes externas permanece
praticamente constante.
- A região central se torna opaca
quando a densidade central atinge cerca de
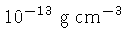 ,
e o subsequente aumento na densidade produz aumento adiabático
na temperatura.
,
e o subsequente aumento na densidade produz aumento adiabático
na temperatura.
- Desta forma a pressão aumenta e
o colapso em queda livre chega ao fim, formando um
núcleo central em equilíbrio hidrostático,
com
densidade central de cerca de
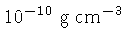 ,
temperatura central
,
temperatura central
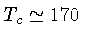 K e massa de somente 0,01 MSol.
K e massa de somente 0,01 MSol.
- As camadas externas
continuam sendo acretadas ao núcleo. Este núcleo é
chamado de proto-estrela.
- Quando a temperatura central
atinge cerca de 2000 K, o hidrogênio, que estava na forma
molecular (
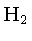 ), se dissocia e como parte
da energia de contração é utilizada na dissociação,
o equilíbrio hidrostático não é mais mantido, e
a proto-estrela colapsa novamente.
), se dissocia e como parte
da energia de contração é utilizada na dissociação,
o equilíbrio hidrostático não é mais mantido, e
a proto-estrela colapsa novamente.
- Quando praticamente
todo o hidrogênio central está na forma atômica,
o núcleo torna-se dinamicamente estável novamente,
atingindo uma densidade de cerca de
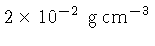 e
e
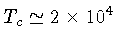 K. Para um observador externo,
a nuvem continua como um objeto infra-vermelho enquanto
o envelope for opaco à radiação visível.
K. Para um observador externo,
a nuvem continua como um objeto infra-vermelho enquanto
o envelope for opaco à radiação visível.
- Com o acréscimo de matéria ao núcleo, o envelope vai
se tornando transparente, até a fotosfera atingir a
superfície do núcleo em equilíbrio hidrostático.
Para uma estrela de 1 MSol, o colapso dura cerca
de 1 milhão de anos.
- As reações nucleares iniciam, mas a luminosidade é
ainda dominada pela contribuição da contração.
- A proto-estrela torna-se completamente convectiva, chegando
ao limite de Hayashi, tornando-se uma estrela visível,
a maior parte em equilíbrio hidrostático, mas ainda contraindo-se,
fora de equilíbrio térmico.
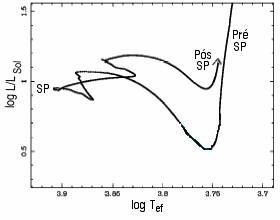
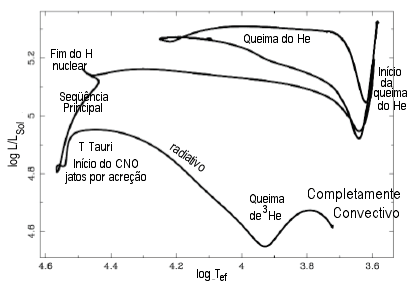 Diagramas HR com os
caminhos evolucionários para um modelo de duas massa solar (esquerda)
descendo a trajetória de Hayashi,
e um de 30 massas solares após a chegada a base da trajetória
de Hayashi.
Diagramas HR com os
caminhos evolucionários para um modelo de duas massa solar (esquerda)
descendo a trajetória de Hayashi,
e um de 30 massas solares após a chegada a base da trajetória
de Hayashi.
- Descendo a trajetória de Hayashi, a contração
ocorre em escala de tempo térmica, 104 a 105
anos. A transformação de 2D em 3He ocorre
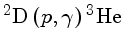 durante esta descida, pois requer só 105K, reduzindo
a velocidade com que a estrela desce a trajetória. A maior
parte do 3He é primordial (do Big-Bang),
já que a abundância de 2D é muito pequena.
A acresção se dá através de um disco.
durante esta descida, pois requer só 105K, reduzindo
a velocidade com que a estrela desce a trajetória. A maior
parte do 3He é primordial (do Big-Bang),
já que a abundância de 2D é muito pequena.
A acresção se dá através de um disco.
Günther Wuchterl & Werner M. Tscharnuter, publicaram no
Astronomy
& Astrophysics, 398, 1081, de 2003,
seus cálculos autoconsistentes de colapso protoestelar e pré-seqüência
principal, mostrando que seus modelos de estrelas de 2MSol
estão próximos dos cálculos anteriores, quando os efeitos
dinâmicos de acresção de massa tornam-se desprezíveis, mas que os modelos de
1MSol nunca tornam-se completamente convectivos e
são aproximadamente 1 milhão de anos mais velhos que os modelos
calculados assumindo equilíbrio hidrostático desde o início.
As observações indicam que existe uma grande variedade
de condições iniciais na formação de estrelas, já que
existe uma grande dispersão nas velocidades de rotação das
estrelas pré-sequência principal
(Anita
Krishnamurthi,
Marc H. Pinsonneault, S. Barnes & S. Sofia, 1997, Astrophysical Journal,
480, 303).
| Evolução de uma pré-estrela do tipo solar |
| Estágio |
Tempo aproximado até o próximo estágio (anos) |
Tcentral (K) |
Tsuperficial (K) |
Densidade central (partículas/m3) |
Diâmetro* (km) |
Tipo de objeto |
| 1 |
2 x 106 |
10 |
10 |
109 |
1014 |
Nuvem interestelar |
| 2 |
3 x 104 |
100 |
10 |
1012 |
1012 |
Nuvem |
| 3 |
105 |
10,000 |
100 |
1018 |
1010 |
Nuvem/Proto-estrela |
| 4 |
106 |
1,000,000 |
3000 |
1024 |
108 |
Proto-estrela |
| 5 |
107 |
5 000 000 |
4000 |
1028 |
107 |
Proto-estrela |
| 6 |
3 × 107 |
10,000,000 |
4500 |
1031 |
2 ×106 |
Estrela |
| 7 |
1010 |
15 000 000 |
6000 |
1032 |
1,5 × 106 |
Estrela na seqüência principal |
*diâmetro do Sol=1,4 ×106 km, sistema solar=1,5 ×1010 km. |
| Massa | Tempo até ZAMS |
|---|
| (MSol | (anos) |
|---|
| 30 | 10 mil |
| 1 | 30 milhões |
| 0,2 | 1 bilhão |
Embora o lítio seja destruído para temperaturas acima de 2,5 milhões de K,
Alastair Graham Walker Cameron (1925-2005) & William Alfred Fowler (1911-1995) demonstraram em 1971 no Astrophysical
Journal, 164, 111, que o lítio pode ser produzido no Ramo Assimptótico
das Gigantes, quando o Be formado nos flashes rápidos de He decai em Li.
Yong Shi, Lee Armus, George Helou, Sabrina Stierwalt, Yu Gao, Junzhi Wang, Zhi-Yu Zhang &; Qiusheng Gu,
2014, arXiv1410.5504
demonstram que as galáxias com baixa metalicidade são muito ineficientes na formação estelar.
Modelos de Pré-Sequência Principal de Pisa





Próxima: Formação e Campo Magnético
Próxima: Estrelas Binárias
Volta: Interiores Estelares
Anterior: Tolman-Oppenheimer-Volkoff
©
Modificada em 22 out 2014


 Glóbulos de Bok absorvendo luz no centro da
nebulosa de emissão e região de formação
estelar NGC 281. Imagem obtida com a
Advanced Camera for Surveys do Telescópio Espacial Hubble
em outubro de 2005. A nebulosa está localizada a 9500 anos-luz de
nós, na direção da constelação da
Cassiopéia.
Glóbulos de Bok absorvendo luz no centro da
nebulosa de emissão e região de formação
estelar NGC 281. Imagem obtida com a
Advanced Camera for Surveys do Telescópio Espacial Hubble
em outubro de 2005. A nebulosa está localizada a 9500 anos-luz de
nós, na direção da constelação da
Cassiopéia.
 e portanto a formação estelar tem que se dar com a
formação de um disco de acresção; a viscosidade
no disco permite
a acresção de massa ao centro, enquanto parte da massa é
acelerada para as partes externas, pela conservação
do momentum angular; ao mesmo tempo,
o disco é truncado no centro pelo
campo magnético, e matéria ionizada
tem que ser expelida por ejeção magneto-centrífuga,
possivelmente na forma de jatos bipolares,
por conservação do campo magnético,
como na imagem ao lado do objeto Herbig-Haro 30
[George Howard Herbig (1920-2013)
(1950, Astrophysical
Journal, 111, 11)
e Guillermo Haro (1913-1988) (1952, Astrophysical Journal, 115, 572)],
obtida com o Telescópio Espacial Hubble.
As nebulosas Herbig-Haro correspondem aos jatos colimados,
e suas (proto) estrelas têm discos circum-estelares e
são mais jovens que 100 milhões de anos.
e portanto a formação estelar tem que se dar com a
formação de um disco de acresção; a viscosidade
no disco permite
a acresção de massa ao centro, enquanto parte da massa é
acelerada para as partes externas, pela conservação
do momentum angular; ao mesmo tempo,
o disco é truncado no centro pelo
campo magnético, e matéria ionizada
tem que ser expelida por ejeção magneto-centrífuga,
possivelmente na forma de jatos bipolares,
por conservação do campo magnético,
como na imagem ao lado do objeto Herbig-Haro 30
[George Howard Herbig (1920-2013)
(1950, Astrophysical
Journal, 111, 11)
e Guillermo Haro (1913-1988) (1952, Astrophysical Journal, 115, 572)],
obtida com o Telescópio Espacial Hubble.
As nebulosas Herbig-Haro correspondem aos jatos colimados,
e suas (proto) estrelas têm discos circum-estelares e
são mais jovens que 100 milhões de anos.
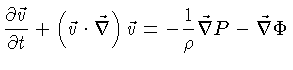
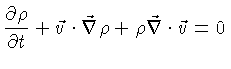
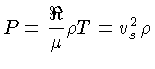
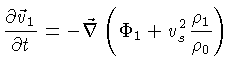
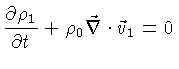
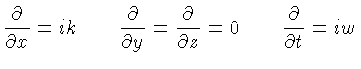
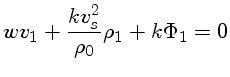
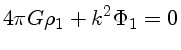
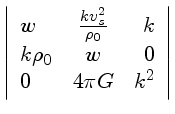
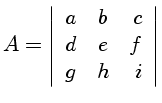
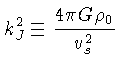
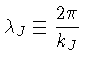
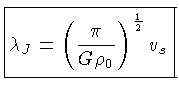
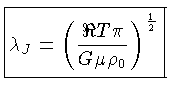
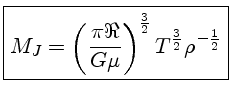
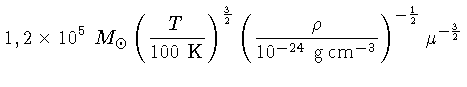
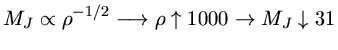 e ocorre fragmentação
e ocorre fragmentação
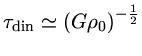 é da ordem de
é da ordem de 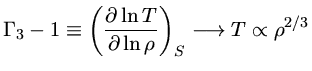
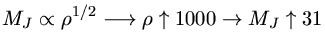 e não ocorre fragmentação
e não ocorre fragmentação
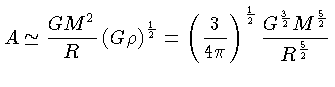
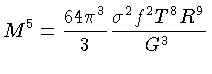
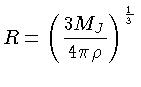
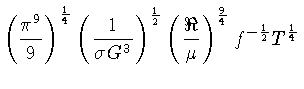
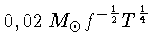
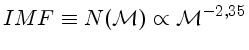
 O esfriamento das nuvens interestelares se dá principalmente
através da excitação colisional dos metais para níveis
proibidos, isto é, que se desexcitam principalmente por
emissão de fótons. Estes fótons têm níveis
de energia que não podem ser absorvidos normalmente,
e a energia é perdida da nuvem. Nas regiões HII as linhas
de O2+ dominam,
no gás neutro as linhas de
C+
e
Fe+,
e no gás molecular as linhas de
H2.
A formação de moléculas torna o gás mais denso porque o número
de partículas é reduzido.
Mas a formação de
H2
se dá principalmente por
catalização de grãos de poeira, produzidos pelas
estrelas de População I e II e retornados ao meio interestelar
por ventos e explosões.
Quanto mais metálico o gás, mais rápido ele esfria.
Sem metais (Pop. III) a fragmentação não ocorre porque o esfriamento é pequeno,
e a contração adiabática
(Richard B. Larson).
Raffaella Schneider, Kazuyuki Omukai, Simone Bianchi & Rosa Valiante
publicaram no Monthly Notices of the Royal Astronomical
Society, de 28 out 2011 uma estimativa de que
a fragmentação abaixo de 10 massas solares só ocorre
quando a quantidade de grãos de poeira excede 2,6-6,3×10-9
da quantidade de gás.
O esfriamento das nuvens interestelares se dá principalmente
através da excitação colisional dos metais para níveis
proibidos, isto é, que se desexcitam principalmente por
emissão de fótons. Estes fótons têm níveis
de energia que não podem ser absorvidos normalmente,
e a energia é perdida da nuvem. Nas regiões HII as linhas
de O2+ dominam,
no gás neutro as linhas de
C+
e
Fe+,
e no gás molecular as linhas de
H2.
A formação de moléculas torna o gás mais denso porque o número
de partículas é reduzido.
Mas a formação de
H2
se dá principalmente por
catalização de grãos de poeira, produzidos pelas
estrelas de População I e II e retornados ao meio interestelar
por ventos e explosões.
Quanto mais metálico o gás, mais rápido ele esfria.
Sem metais (Pop. III) a fragmentação não ocorre porque o esfriamento é pequeno,
e a contração adiabática
(Richard B. Larson).
Raffaella Schneider, Kazuyuki Omukai, Simone Bianchi & Rosa Valiante
publicaram no Monthly Notices of the Royal Astronomical
Society, de 28 out 2011 uma estimativa de que
a fragmentação abaixo de 10 massas solares só ocorre
quando a quantidade de grãos de poeira excede 2,6-6,3×10-9
da quantidade de gás.


 Outra nuvem molecular é Sagittarius B-2
Outra nuvem molecular é Sagittarius B-2




