Da equação de velocidade se pode deduzir facilmente a
velocidade de escape do sistema, que representa a
velocidade mínima para que o corpo escape da atração
gravitacional do sistema.
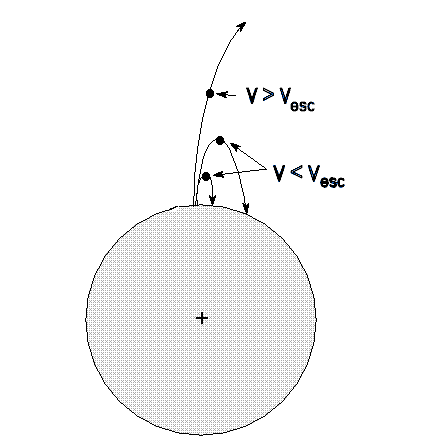
A velocidade de escape é por definição
aquela com a qual o corpo chega com velocidade zero no infinito
(v = 0 em r = ∞),
o que representa um órbita
parabólica, já que
ε = 0. Assim, uma órbita parabólica pode ser
considerada uma órbita elíptica com e = 1 e
a = ∞.
Neste caso,
Para um órbita hiperbólica, a energia total é positiva; a energia
cinética é tão grande que a partícula pode escapar do sistema e se
afastar dele. A parábola é o caso limite entre
a órbita fechada (elipse) e a hipérbola. Halley, usando o método
de Newton, encontrou que vários cometas têm órbita parabólica.
Simulação
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: Problema de muitos corpos
Próxima: Exemplos
Volta: A equação da energia
Anterior: Velocidade Circular
©
Modificada em 30 jun 1998

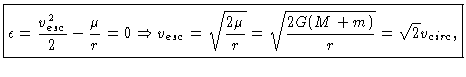
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)