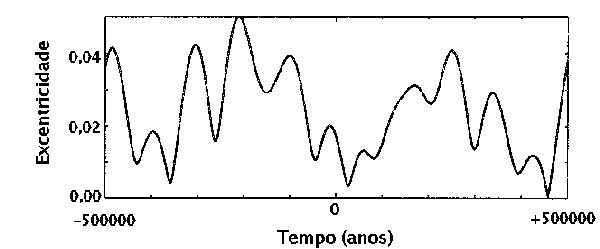
Variação da excentricidade da órbita da Terra em torno do Sol devido aos efeitos de muitos corpos.
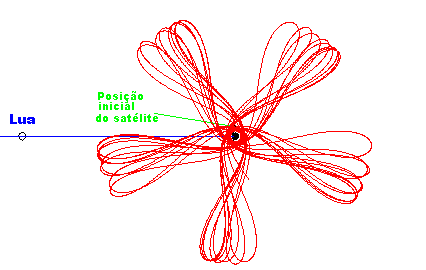
Simulação da órbita de um satélite em torno da Terra devido à influência da Lua.
Consideramos até aqui que a órbita é um problema de dois corpos perfeitamente esféricos. O Teorema das Cascas Esféricas, de Newton (Isaac Newton, 1687. Philosophiae Naturalis Principia Mathematica, London, p. 193, Theorem XXXI), demonstra que corpos com simetria esférica podem ser representados como se toda sua massa estivesse no seu centro. Na realidade, os planetas interferem entre si, perturbando a órbita dos outros. Ainda assim suas órbitas não se desviam muito das cônicas, só que os elementos da órbita variam com o tempo e precisam ser calculados por aproximações sucessivas, pois a órbita não pode ser resolvida analiticamente. Para a órbita da Terra em torno do Sol, como a massa do Sol é 1047 vezes maior que a massa de Júpiter e Júpiter está 5,2 vezes mais distante do que o Sol, a força gravitacional de Júpiter sobre a Terra é 28 mil vezes menor que a do Sol e, portanto, seu efeito pode ser calculado pelo método das pertubações.
Além disto, mesmo para só dois corpos macroscópicos, com a Terra e a Lua, a solução de dois corpos não é exata, pois nem a Terra nem a Lua são esferas perfeitas e, portanto, não se comportam como massas pontuais. Mais ainda, devido às marés, a Terra e a Lua não são sequer rígidas. O momento de quadrupolo da Terra e da Lua causam perturbações tanto perpendiculares ao plano da órbita quanto radiais.


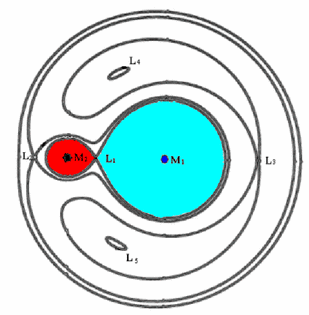
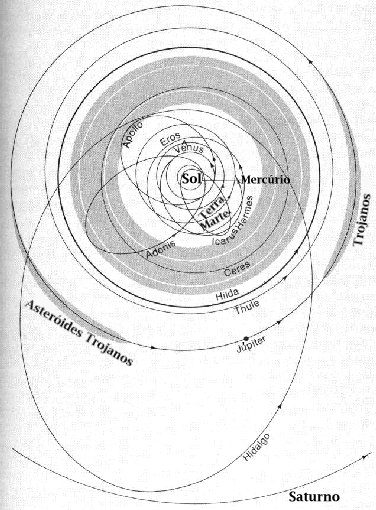
Seu sucessor foi o matemático nascido na Sardinia, atual Itália, Giuseppe Lodovico Lagrangia, que publicou com o nome francês de Joseph-Louis Lagrange (1736-1813), estudando porque a Lua apresenta sempre a mesma face para a Terra e definindo os cinco pontos de Lagrange de um sistema de dois corpos, que são soluções para o problema restrito de três corpos, um corpo de massa desprezível no mesmo plano de um sistema de dois corpos, resultando em tres corpos na mesma linha ou formando os ápices de um triângulo equilateral (60° antes e depois da órbita dos corpos massivos), como nos asteróides Jovianos e Trojanos. No seu livro Méchanique Analytique de 1788 introduziu a Equação de Euler-Lagrange (L=Ecin-U) e o conceito de energia total, cinética e potencial (E=Ecin+U). Note que todos os termos são escalares.
O matemático francês Alexis Claude Clairaut (1713-1765), em seu livro de 1743, A Teoria da Forma da Terra, estudando o equilíbrio de fluídos e a força gravitacional em elipsóides em revolução, concluiu que a Terra não é esferica, mas um elipsoide achatado nos polos. Juntamente com o matemático francês Pierre Louis Moreau de Maupertuis (1698-1759), Clairaut foi em uma expedição para a Lapônia (67°N, círculo polar norte), na Finlândia, em 1735 para medir este achatamento. Se a Terra fosse perfeitamente esférica, um grau medido verticalmente ao longo do meridiano deveria ser o mesmo em todos os pontos da Terra. Eles demonstraram que esta distância era maior próximo ao polo. O diâmetro equatorial da Terra é 12,756,3 km, enquanto o diâmetro polar é 12.713,5 km. A diferença de 42,8 km deve-se ao fato da Terra ter a forma de um geóide. Maupertis demonstrou depois o princípio de ação mínima, que diz que a ação (s=massa×velocidade×distância) associada ao movimento de uma partícula ou um grupo de partículas deve ser mínima ao longo do caminho verdadeiro da partícula (ds=0).
O matemático francês Pierre-Simon Laplace (1749-1827), em seu livro de 1796 Exposition du système du monde propôs a origem do Sol e dos planetas a partir de uma nebulosa, detalhado em seu compêndio de astronomia matemática de cinco volumes Traité de Mécanique Céleste, publicado entre 1799 e 1825. Nele, passando da mecânica clássica baseada em geometria para o cálculo integral e de diferenças finitas, mostrou que supondo que o Sistema Solar consiste de um conjunto de corpos rígidos movendo-se no vácuo, os movimentos planetários eram estáveis, levando a prova até os cubos das excentricidades e das inclinações. No terceiro volume introduziu os harmônicos esféricos. Com seus trabalhos sobre a teoria das probabilidades, Théorie analytique des probabilités de 1812 e Essai philosophique sur les probabilités de 1814, demonstrou que o fato dos planetas girarem praticamente no mesmo plano e suas rotações também serem na maior parte na mesma direção, indica que o Sistema Solar se formou junto, de uma nuvem em rotação. Laplace acreditava no determinismo, propondo que se alguém conhecesse todas as posições e forças (estados) de um sistema, poderia determinar seu passado e seu futuro. Ministro do Interior de Napoleão Bonaparte (1769-1821) por somente seis semanas, foi demitido como geometra de primeira categoria mas administrador medíocre e entra para o senado, tornando seu presidente. Em 1817 foi nomeado Marquês de Laplace pelo rei Luís XVIII (1755-1824) - o "Desejado" - após a derrota de Napoleão em 1814 e novamente em 1815 (Batalha de Waterloo), em reconhecimento à sua contribuição científica e política. Foi um dos primeiros a reconhecer a possível existência de buracos negros, concebidos pelo físico, astrônomo e geólogo britânico John Michell (1724-1793), como corpos em que a gravidade é tão grande que nem a luz terá velocidade suficiente para escapar.
De acordo com o astrônomo francês Hervé Auguste Étinne Albans Faye (1814-1902): Quando Laplace presenteou ao general Bonaparte a primeira edição de seu livro Exposition du Système do monde, Napoleão teria lhe dito: "Newton falou de Deus em seu livro. Eu já percorri o seu e não identifiquei nenhuma menção a ele." Laplace teria respondido: "Cidadão Primeiro Consul, eu não tive necessidade desta hipótese."
Em 13 de março de 1781, ocorreu a descoberta do sétimo planeta a partir do Sol, Urano, quando o professor de música e construtor de telescópios alemão Friedrich Wilhem Herschel (1738-1822) observou um objeto curioso próximo à estrela τ Tauris e observou seu movimento quatro dias depois. Ele já havia sido observado em 1690, pelo astrônomo inglês John Flamsteed (1646-1719) e entre 1750 e 1769 pelo astrônomo francês Pierre Leminnier (1675-1757), mas foi erroniamente catálogado como uma estrela pelo primeiro (34 Tauri). Sir William Herschell comunicou sua descoberta ao astrônomo real britânico Nevil Maskelyne (1732-1811) que o observou e reportou que poderia ser um planeta regular com órbita quase circular, ou um cometa em uma elipse bem excêntrica. O astrônomo russo Anders Johan Lexell (Andrei Ivanovich Leksel, 1740-1784) foi o primeiro a calcular sua órbita, circular, descartando a hipótese de um cometa. O astrônomo alemão Johan Elert Bode (1747-1826), diretor do Observatório de Berlim, também calculou sua órbita e sugeriu o nome Urano.
Contemporâneo de Laplace foi o astrônomo, matemático e físico alemão Johann Carl Friedrich Gauss (1777-1855), primeiro diretor do Observatório de Göttingen (1807). O padre e astrônomo italiano Giuseppe Piazzi (1746-1826) havia descoberto o planeta anão Ceres em 1801, então suposto como o oitavo planeta, na posição prevista pela lei de Titius-Bode [Rn=4+(3+2n), Johan Daniel Tietz (1729-1796)]. O filósofo alemão Georg Wilhelm Friedrich Hegel (1770-1831), que propunha que tudo poderia ser determinado pela razão, criticou veemente a descoberta dizendo que só poderiam haver 7 planetas, como em sua tese de habilitação. Mas Ceres era de muito difícil observação, só foi observado por 9°, 2,5% da órbita, e sua redescoberta 20 anos depois só foi possível com a determinação de sua órbita com estes pouquíssimos dados por Gauss, publicados em 1809 no Theoria motus corporum coelestium (Teoria do Movimento dos Corpos Celestiais Girando em Volta do Sol), com uma detalhada explicação sobre a determinação das órbitas dos planetas e cometas. Em 1835 elaborou a Lei de Gauss, que estabelece a relação entre a carga elétrica dentro de um volume e o fluxo elétrico que passa pela superfície deste volume, provada matematicamente por Laplace.
O físico e matemático francês Siméon Denis Poisson (1781-1840) publicou em 1809 Sur les inégalités séculaires des moyens mouvements des planètes e Sur la variation des constantes arbitraires dans les questions de mécanique, no Journal of the École Polytechnique e em 1827 Sur le mouvement de la terre autour de son centre de gravité, no Mémoires de l'Académie, com a correção para o potencial de Laplace,
Em 1833 o matemático irlandês William Rowan Hamilton (1805-1865) generalizou o princípio de mínima ação para incluir a energia e o tempo, criando o Hamiltoniano, basicamente a energia total do sistema (H=Ecin+U), e a variação temporal das energias cinéticas e potenciais, interligadas. Sua solução é o conjunto de possíveis estados compatíveis com a energia total de um sistema.
Com a Mecânica Celeste, o planeta Netuno foi predito matematicamente antes de ser observado diretamente, por desvios observados na órbita de Urano. A predição foi feita pelo matemático francês Urbain Jean Joseph Le Verrier (1811-1877) e a descoberta em 23-24 de setembro de 1846 no Observatório de Berlin pelo astrônomo Johann Gottfried Galle (1812-1910), dentro de 1° da previsão de Le Verrier. Existem evidências que Galileo o registrou em 1613 [Charles T. Kowal (2008), "Galileo's Observations of Neptune", The International Journal of Scientific History. DIO. 15], Joseph Jérome Lefrançois Lalande (1732-1807) em 1795 e Sir John Frederick William Herschel (1792-1871) em 1830, mas nenhum deles o reconheceu como um planeta, por seu baixo movimento. As observações de Netuno no fim do século XIX levaram alguns astrônomos a especular que sua órbita poderia estar sendo afetada por outra planeta externo, o que sabemos atualmente eram imprecisões nas observações. Estas especulações levaram o empresário americano Percival Lowell (1855-1916) a fundar um observatório para a procura deste nono planeta, que Lowell chamou de planeta X [Clyde William Tombaugh (1946). "The Search for the Ninth Planet, Pluto". Astronomical Society of the Pacific Leaflets. 5, 73-80] mas até sua morte nada encontraram. As buscas reiniciaram em 1929 e, em 18 de fevereiro de 1930, usando um comparador de piscada (blink comparator, inventado pelo físico Carl Pulfrich da Carl Zeiss A.G.), que permite a troca rápida de duas fotografias para detectar diferenças, Clyde William Tombaugh (1906-1997) descobriu Plutão como um objeto movendo-se nas suas placas de 23 e 29 de janeiro de 1930. Como a massa de Plutão é muito pequena para afetar a órbita de Netuno, a descoberta foi acidental e, porisso, demorou tanto. Hoje em dia existem muitos planetas anões como Plutão conhecidos.
Cálculos das órbitas dos planetas
Circular 179 da IAU sobre o cálculo
das efemérides
Uma lenda da internet é que os sumérios teriam proposto a existência de um décimo planeta, que eles chamaram de Niburu, com massa suficiente para perturbar a órbita da Terra, o que é totalmente incompatível com as observações atuais.
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)