Podemos deduzir a equação da energia calculando-se
o valor do momentum angular e da energia no periélio,
já que são constantes. No periélio:
rp = a(1 - e),
h = rpvp,
já que, neste ponto, 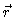 p
e
p
e 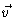 p
são perpendiculares entre si.
Para a energia (eq. 2), temos:
Por outro lado, da
definição do semi-lactus rectum p, temos
Substituindo-se h e rp na equação de energia ε,
temos:
pois
(1 - e)(1 + e) = 1 - e2,
que é válido
para qualquer órbita cônica e
mostra que o semi-eixo maior da órbita só depende da
energia do sistema.
p
são perpendiculares entre si.
Para a energia (eq. 2), temos:
Por outro lado, da
definição do semi-lactus rectum p, temos
Substituindo-se h e rp na equação de energia ε,
temos:
pois
(1 - e)(1 + e) = 1 - e2,
que é válido
para qualquer órbita cônica e
mostra que o semi-eixo maior da órbita só depende da
energia do sistema.
ε < 0 → a > 0
elipse
ε = 0 →
a = ∞
parábola
ε > 0 → a < 0
hipérbole
Vamos agora calcular a velocidade em qualquer ponto da órbita. Da definição de semi-lactus rectum p,
Como a energia é definida por (8),
Escrevendo a excentricidade em termos da energia:
e =
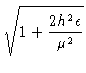
.
Logo, se:
Das
equações de energia (2)
e (8), vemos que
logo
que é a equação da velocidade do sistema em qualquer ponto r da órbita.
 Astronomia e Astrofísica
Astronomia e Astrofísica

![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: Velocidade Circular
Volta: Leis de Kepler Generalizadas
Anterior: Terceira lei de Kepler: Lei harmônica
©
Modificada em 8 abril 2000
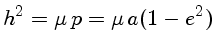
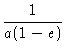
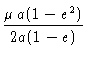 -
- 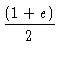 - 1
- 1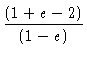
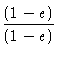 ,
,
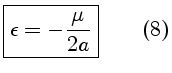
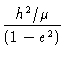 .
.
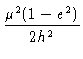 .
.
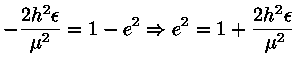
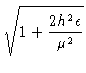 .
.
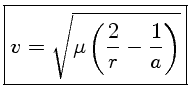
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)