A partir da conservação do momentum angular (3),
e escrevendo em coordenadas polares,
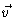 = d
= d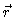 /dt = r d
/dt = r d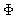 /dt
/dt 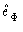 +dr/dt êr, onde
+dr/dt êr, onde
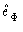 é o vetor
unitário na direção de
é o vetor
unitário na direção de 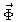 e
e
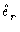 o vetor unitário na direção de
o vetor unitário na direção de 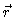 ,
temos
,
temos
Como 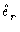 e
e
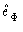 são perpendiculares entre si por construção, segue que
são perpendiculares entre si por construção, segue que
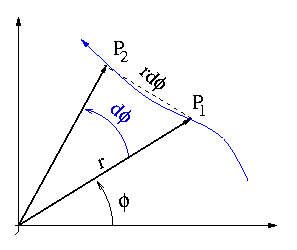
Sejam P1 e P2 duas posições sucessivas do corpo num
intervalo δt.
O elemento de área nesse intervalo de tempo é:
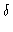 A
A =
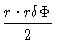
,
ou
Para
δt 0,
Como a conservação do momentum angular (eq. 3) prova que h, é
uma constante, dA/dt é uma constante, que é a lei
das áreas. A lei das áreas de Kepler é portanto
um consequência direta da lei de conservação
do momentum angular.
0,
Como a conservação do momentum angular (eq. 3) prova que h, é
uma constante, dA/dt é uma constante, que é a lei
das áreas. A lei das áreas de Kepler é portanto
um consequência direta da lei de conservação
do momentum angular.
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: Terceira lei de Kepler: Lei harmônica
Volta: Leis de Kepler Generalizadas
Anterior: Primeira lei de Kepler: Lei das
©
Modificada em 18 Out 1999
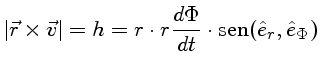
![]() e
e
![]() são perpendiculares entre si por construção, segue que
são perpendiculares entre si por construção, segue que
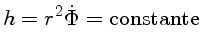
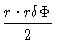 ,
,
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)