Duas relações das elipses são (ver
Área de uma elipse):
A = πab,
onde A é a área, a o semi-eixo maior e b o semieixo menor,
e
b =
a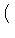
1 - e
2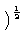
.
Da lei das áreas (eq. 5), temos:
dA =
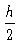 dt
dt.
Integrando-se sobre um período, P,
πab =
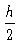 P
P
(6)
Substituindo-se b acima, e a definição do semi-lactus rectum p,
b =
a
(1 - e
2)
1/2
= (pa)
1/2 =
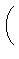
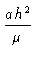
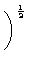
.
Elevando-se (6) ao quadrado:
ou
P
2 =
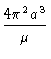
.
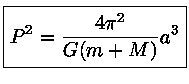
(7)
Desta forma fica demonstrado que as tres leis de Kepler podem
ser deduzidas das leis de Newton.
A "constante" de Kepler depende portanto da soma das massas dos
corpos. No caso dos planetas do sistema solar,
que orbitam o Sol, esta soma é praticamente igual
à massa do Sol (já que a massa de Júpiter, o maior planeta, é menor que um milésimo da massa do Sol) e, portanto, aproximadamente constante.
Na secção (Newton) vimos como a
3a lei de Kepler na forma derivada
por Newton é usada para
determinar massas de corpos astronômicos.
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: A equação da energia
Volta: Leis de Kepler Generalizadas
Anterior: Segunda lei de Kepler: Lei das
©
Modificada em 6 abril 2000
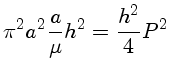
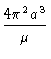 .
.
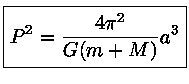 (7)
(7)
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)