e escrevendo em coordenadas polares,
, onde 
é o vetor
unitário na direção de 
. Como
e 
são perpendiculares entre si, temos:
A partir da conservação do momentum angular (3),
e escrevendo em coordenadas polares, , onde é o vetor
unitário na direção de . Como
e
são perpendiculares entre si, temos:
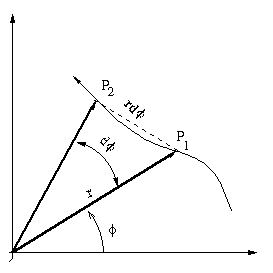
Sejam 
e 
duas posições sucessivas do corpo num
intervalo 
. O elemento de área neste espaço
de tempo é:
ou
Para 
,
Como a conservação do momentum angular (3) prova que h é
uma constante, dA/dt é uma constante, que é a lei
das áreas. A lei das áreas de Kepler é portanto
um consequência direta da lei de conservação
do momentum angular.
Introdução à Astronomia e à
Astrofísica
