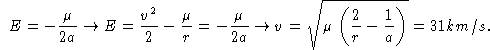Duas relações das elipses são (veja o apêndice):

onde A é a área, a o semi-eixo maior e b o semieixo menor,
e

Da lei das áreas, (5), temos:

Integrando-se sobre um período, P,

Substituindo-se b acima, e a definição do semi-lactus rectum,
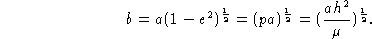
Elevando-se (6) ao quadrado:

ou

Esta é a terceira lei de Kepler, generalizada por Newton,
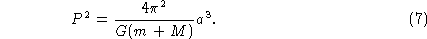
Desta forma fica demonstrado que as tres leis de Kepler podem
ser deduzidas das leis de Newton.
A ``constante'' de Kepler depende portanto da soma das massas dos
corpos. No caso dos planetas do sistema solar,
que orbitam o Sol, esta soma é praticamente igual
à massa do Sol, e portanto aproximadamente constante.
Podemos calcular o valor das constantes, calculando-se
o valor do momentum angular e da energia no periélio,
já que são constantes. No periélio:


já que 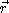 e
e 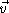 são perpendiculares entre si.
Para a energia (2), temos:
são perpendiculares entre si.
Para a energia (2), temos:
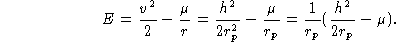
Por outro lado, da definição do semi-lactus rectum, temos
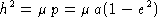 . Substituindo-se h e
. Substituindo-se h e 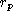 em E, temos:
em E, temos:
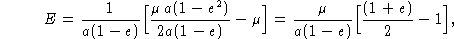
pois 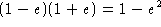 ,
,
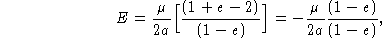

que é válido
para qualquer órbita cônica e
mostra que o semi-eixo maior da órbita só depende da
energia do sistema.
Da definição de semi-lactus rectum p,
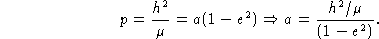
Como a energia é definida por (8),
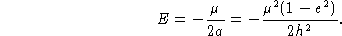
Escrevendo a excentricidade em termos da energia:
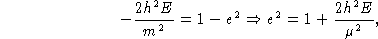

Logo, se:



Das equações (2) e (8), vemos que
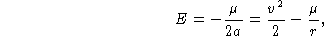
logo

que é a equação da velocidade do sistema.
Da equação de velocidade se pode deduzir facilmente a
velocidade de escape do sistema, que representa a
velocidade mínima para que o corpo escape da atração
gravitacional do sistema. Esta velocidade é por definição
aquela com a qual o corpo chega com velocidade zero no infinito
(v=0 em  ), o que representa um órbita
parabólica, já que E=0. Neste caso,
), o que representa um órbita
parabólica, já que E=0. Neste caso,
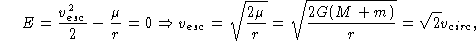
já que da definição de velocidade e de órbita circular (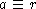 ):
):
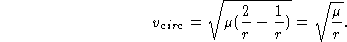
Para um órbita circular, vemos que a energia total é negativa, já
que:
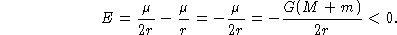
Para um órbita hiperbólica, a energia total é positiva; a energia
cinética é tão grande que a partícula pode escapar do sistema e
se
afastar dele. A parábola é o caso limite entre
a órbita fechada (elipse) e a hipérbole. Halley, usando o método
de Newton, encontrou que vários cometas têm órbita parabólica.
Assumimos até aqui que a órbita é um problema de dois corpos. Na
realidade, os planetas interferem entre si, perturbando a órbita dos
outros. Ainda assim suas órbitas não se desviam muito das cônicas,
só que os elementos da órbita variam com o tempo e precisam ser
calculados por aproximações sucessivas, pois a órbita não
pode ser resolvida analiticamente. Além disto, mesmo só para dois corpos
macroscópicos, com a Terra e a Lua, a solução de dois corpos não
é exata, pois nem a Terra nem a Lua são esferas perfeitas, e portanto
não se comportam como massas pontuais. Mais ainda, devido às marés,
a Terra e a Lua não são sequer rìgidas.
Exemplos:
1) O Cometa Austin (1982g) se move em uma órbita parabólica.
Qual foi sua velocidade em 8 de outubro de 1982, quando estava a
1,1 UA do Sol?
Como a órbita é parabólica, E=0, logo:
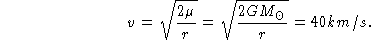
2) o semi-eixo do planetóide 1982RA é de 1,568UA e sua distância
ao Sol em 8 de outubro de 1982 era de 1,17 UA. Qual era sua velocidade?
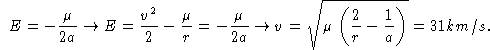
Próxima: Apêndice: Propriedades de uma elipse
Volta: Problema de dois corpos
Anterior: Segunda lei de Kepler
 Introdução à Astronomia e à
Astrofísica
Introdução à Astronomia e à
Astrofísica

kepler@if.ufrgs.br
Modificada em 27 Out 1997