5. SOLUCIÓN FORMAL DE LA ECUACIÓN DEL TRANSPORTE  

       RADIATIVO

 

Vamos ahora a considerar el caso general de una fotosfera en la cual existe material en condiciones de absorber y emitir radiación. Nuestro propósito es encontrar una solución general de la ecuación del transporte radiativo (7.13), obtenida para una atmósfera plano-paralela. Haciendo nuevamente la sustitución m = cos q, la ecuación a resolver es la siguiente :

 

 

                                                                                                  (7.18)

 

 

Se trata pues de una ecuación diferencial lineal, de primer orden y con  coeficientes constantes. Para encontrar la solución general multiplicamos ambos miembros de (7.18) por el factor de extinción  y dividimos luego por la variable m. Así obtenemos :

 

 

                                            

 

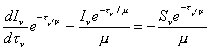
Luego :

 

                                            

 

 

Integrando la ecuación anterior entre dos profundidades ópticas  y  se tiene:

 

 

                           ,

 

 

                          

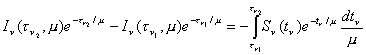en la cual t_n es la profundidad óptica t_n tomada como variable de integración. Multiplicando ambos miembros de la expresión anterior por  y despejando  resulta :

 

 

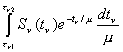                                     (7.19)

                                                                                                                          

 

 

Para comprender el significado físico de la solución general (7.19) regresaremos por un momento a los dos casos particulares antes considerados: la capa de espesor finito y la atmósfera semi-infinita.

 

En el primer caso (capa finita), consideraremos  (frontera superior) y   (frontera inferior). La (7.19) se escribirá ahora de la siguiente manera :

 

 

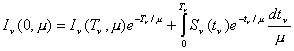                                ,                 (7.20)

 

válida para 0 < m £ 1.

 

El primer término del segundo miembro de (7.20) representa claramente la intensidad específica que alcanza la frontera superior de la capa según la dirección m, proveniente de la frontera inferior cuya profundidad óptica es T_n. La exponencial  es el factor de extinción en la dirección considerada. Por  su parte, el segundo término del segundo miembro de (7.20) representa la intensidad específica monocromática emitida en cada punto de la capa en la dirección considerada, correspondientemente atenuada por el factor de extinción e integrada sobre todo el espesor óptico de la capa. Esta última aseveración se constata fácilmente si se tiene en cuenta la expresión (6.55). En efecto, de acuerdo a esa expresión, el incremento de la intensidad específica dI_n producido por una masa de densidad r  que emite en la dirección de propagación ds es j_nr ds, o bien, j_nr dx/cosq. Si expresamos dx en función de dt_n, el incremento anterior dI_n  debería ser: -S_n dt_n/cosq. La fracción de intensidad creada en cada punto que alcanza la frontera superior de la capa será pues:   Integrando esta última expresión sobre todo el espesor óptico de la capa finita (entre T_n y 0) y cambiando los límites de integración, se obtiene el segundo término del segundo miembro de la expresión (7.20). Si se considera el caso en que ,  y valores de m negativos, se obtiene entonces la expresión de la radiación emergente por la frontera inferior.

 

En el caso particular de que la función fuente S sea constante dentro de la capa y que no haya intensidad incidente sobre la frontera inferior, la (7.20) permite expresar la intensidad de un rayo emergente por la frontera superior, normal a la capa (m = 1), de la siguiente manera :

 

                                                  

 

 

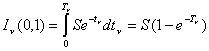
Si T_n >> 1, resulta directamente I_n(0,1) = S. Es decir, si la función fuente es constante en una capa de espesor finito ópticamente gruesa (T_n >> 1) sobre la cual no incide radiación por la frontera inferior, la intensidad específica monocromática que emerge normalmente de dicha capa es igual a la misma función fuente.

 

Para interpretar físicamente la solución (7.19) en el caso de una atmósfera semi-infinita tomaremos  = 0 y haremos tender  a infinito. El primer término de la solución general (7.19) desaparece en este caso en virtud de la condición límite impuesta en (7.14). En consecuencia, se tendrá ahora :

 

 

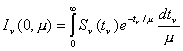                                                                           (7.21)

 

 

Si sólo se consideran valores de m positivos (radiación emergente), la fórmula anterior expresa el hecho de que la intensidad emergente de una atmósfera semi-infinita en una dirección m, está dada por la suma sobre todas las profundidades ópticas t_n de las intensidades generadas en cada profundidad t_n correspondientemente atenuadas por el factor .

 

La ecuación (7.21) constituye la forma integral básica de la ecuación del transporte radiativo. Si pudiésemos resolver esta ecuación estaríamos en condiciones de expresar lo que predice la teoría. Sin embargo, para efectuar la integración en (7.21) debemos conocer de qué manera varía la función fuente con la profundidad óptica t_n. Hemos visto que en ciertos casos S_n  se reduce a funciones simples tales como B(n,T) o J_n. En ocasiones, sin embargo, S_n puede resultar una función muy complicada.

 

A manera de ejemplo ilustrativo, calcularemos la intensidad específica monocromática emergente de una atmósfera semi-infinita caracterizada por una función fuente lineal de la forma :

 

 

                                             S_n (t_n) = a + bt_n                                                      (7.22)

 

Reemplazando (7.22) en (7.21) resulta :

 

                                            

 

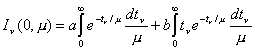
Haciendo el cambio de variables x = t_n/m, se obtiene :

 

 

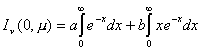                                                                          (7.23)

 

 

La primera de las integrales  del segundo miembro es obviamente la unidad, en tanto que la segunda puede resolverse “por partes”, llamando m = x y dv = e^-x. Dado que con esta sustitución dm = dx y  v = e^-x, resulta :

 

 

 

                                           

 

 

 

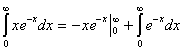
El primer término del segundo miembro se anula ya que al aplicar la regla de L’Hópital resulta :

 

 

                                      

 

 

Por lo tanto, si S_n es una función lineal de la profundidad óptica, la intensidad específica monocromática emergente de la atmósfera semi-infinita resulta una función lineal de la variable m :

 

 

 

                                             I_n(0,m) = a + bm                                                     (7.24)

 

En general, para resolver el problema es necesario conocer la función fuente lo que no siempre es posible.

 

Consideremos ahora un punto arbitrario interior a una atmósfera semi-infinita, ubicado a una profundidad óptica t_n. Supondremos que no incide radiación sobre la superficie de la atmósfera y admitiremos además que es válida la condición de contorno (7.14). La intensidad I_n(t_n,m) resultante en el punto a profundidad óptica t_n y en la dirección considerada debe ser la suma algebraica de las intensidades emergente e incidente  en ese punto, según la dirección considerada (Figura 7-8). Obviamente, m  será positivo y negativo en uno y otro caso, respectivamente.

Consideremos en primer lugar la radiación emergente del punto considerado. Si el ánguloq se mide como indica la Figura 7-8, la radiación emergente corresponde a los valores angulares comprendidos en el intervalo3p/2<q£p/2, o bien 0<m£1. Para poder aplicar la solución general (7.19) consideraremos  y haremos tendera infinito. En ese caso, teniendo en cuenta (7.14), resulta :

 

 

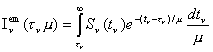                                                        ,                       (7.25)

 

 

válida para losrayos comprendidos en el intervalo0<m £1.

 

Pero el punto considerado también recibe radiación puesto que no se encuentra sobre la frontera superior. Considerando ahora    y, la radiación incidente resulta de (7.19) de la siguiente manera

 

 

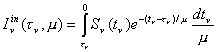          ,                                (7.26)

 

 

 

válida para losrayos comprendidos en el intervalo –1£m<0.

La solución completa de la ecuación del transporte radiativo en un punto cualquiera de una atmósfera estelar semi-infinita, de capas plano-paralelas, estará dada por la suma de (7.25) y (7.26) :

 

 

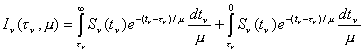         (7.27)

 

Debe tenerse en cuenta que el primer término de la expresión anterior es válido para0<m£1, en tanto que el segundo es válido para –1£m<0. Al igual que antes, para poder conocer la intensidad específica monocromática en un punto cualquiera de una fotosfera es necesario conocer la función fuente.

Al considerar el caso particular de la atmósfera semi-infinita, lo que en verdad nos interesa es poder predecir teóricamente cuál es la intensidad específica monocromática emergente en una cierta dirección. Este resultado, obtenido en(7.21), es muy importante porque nos permite efectuar comparaciones con las observaciones de la superficie solar. No debemos perder de vista que estamos suponiendo que el transporte de energía es sólo radiativo y que las capas fotosféricas son plano-paralela

La (7.21) es una ecuación integral relativamente simple. Lamentablemente, en la mayoría de los casos S_n es una función bastante complicada. Si la función fuente S_nestá dada por la expresión (6.62) puede considerarse relativamente simple, pero aún así existen problemas para conocer el campo radiativo porque S_ndepende de J_n, la que a su vez depende del campo radiante I_n. Estamos pues dentro de un círculo vicioso, motivo por el cual construiremos de otra manera los modelos de atmósferas estelares.