Transformadas de Fourier
Qualquer conjunto de dados pode
ser analisado diretamente por um espectro de freqüências,
ou Transformada de Fourier [desenvolvida por Jean Fourier (1768-1830)
em 1822], pois trata-se de um conjunto
completo e ortonormal de
funções.
Um ponto importante da transformada, é o
critério de Nyquist
[Harry Nyquist (1889-1976),
Certain topics in Telegraph Transmission Theory
(1928, Transactions of the American Institute of Electric Engineers,
47, 617)],
que especifica que um sinal precisa ser amostrado
pelo menos duas vezes em cada ciclo de variação,
isto é, a freqüência de amostragem (freqüência de Nyquist)
precisa ser no
mínimo o dobro da maior freqüência presente no sinal.
Se não for observado o critério, os sinais de mais
alta freqüência serão erroneamente registrados como de
baixa freqüência, fenômeno chamado de alias
(como a impressão da roda girando no sentido inverso
que vemos na televisão).
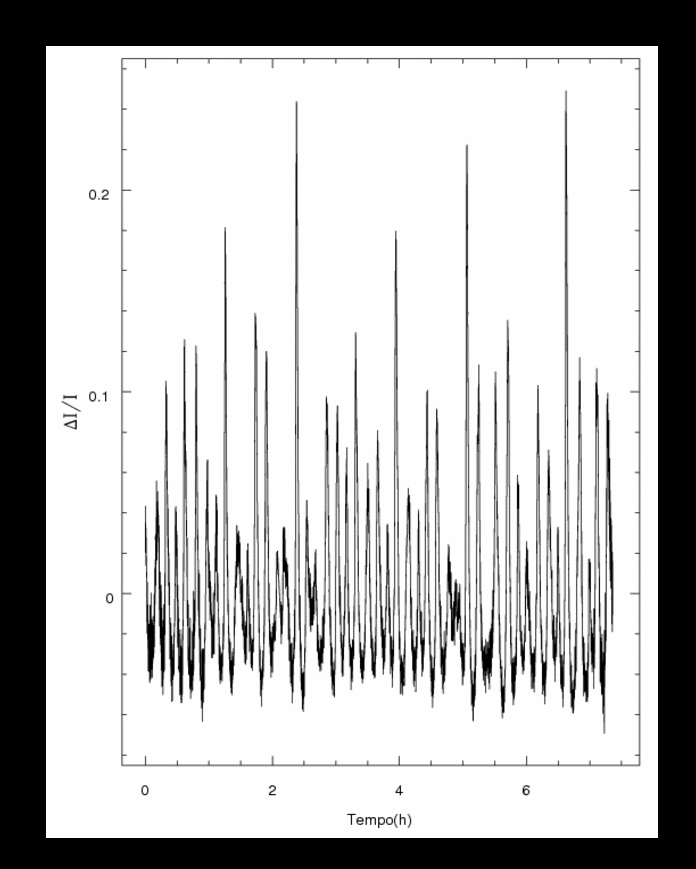
Por exemplo, em imageamento Doppler, onde o fluxo do sangue
é medido por uma série de pulsos ultrasônicos,
se os pulsos não forem repetidos com rapidez suficiente,
um fluxo rápido em uma direção pode ser
interpretado como um fluxo lento na direção oposta.
O limite de Nyquist é importante tanto na baixa freqüência: o tempo
de observação total, T, só pode amostrar períodos menores que T/2,
e de alta freqüência: se o tempo de integração for t, só podemos
medir períodos mais longos que 2t.
A transformada de Fourier de uma função f(x) é definida
como:
![${\cal{F}}[f(x)] \equiv F(w_x) = \int_{-\infty}^\infty
f(x) e^{-2i\pi w_xx} dx$](img195.gif) |
(4.1) |
e a transformada inversa, que recupera a função original é definida como:
![${\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty
F(w_x) e^{2i\pi w_xx} dw_x$](img196.gif) |
(4.2) |
onde 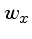 é a freqüência angular,
e
é a freqüência angular,
e
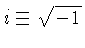 .
.
Para cada freqüência
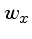 , integramos a função
, integramos a função
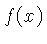 sobre todos os valores da coordenada
sobre todos os valores da coordenada
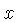 . Se o valor da integral for grande para
esta freqüência, então o sinal tem uma componente significativa
nesta freqüência, isto é, uma parte significativa deste
sinal é composto por esta freqüência.
. Se o valor da integral for grande para
esta freqüência, então o sinal tem uma componente significativa
nesta freqüência, isto é, uma parte significativa deste
sinal é composto por esta freqüência.
Podemos também definir:
![$ \boxed{{\cal{F}}[f(x)] \equiv F(\nu) = \int_{-\infty}^\infty f(x) e^{-i \nu x} dx,}$](img201.gif) |
(4.3) |
e a transformada inversa, que recupera a função original é definida como
:
![$ \boxed{{\cal{F}}^{-1}[F(\nu)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(\nu) e^{i\nu x} d\nu,}$](img202.gif) |
(4.4) |
onde
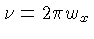 é a freqüência linear.
é a freqüência linear.
Note que:
A condição suficiente para e existência da transformada de Fourier
de uma função 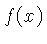 qualquer é que a função seja
integrável, e finita, isto é:
qualquer é que a função seja
integrável, e finita, isto é:
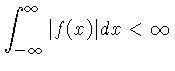 |
(4.5) |
As medidas e imagens que estamos interessados são sempre integráveis e finitas.
Embora os dados (imagens) sejam reais,
a transformada de Fourier é uma função complexa, com
coeficientes reais e imaginários:
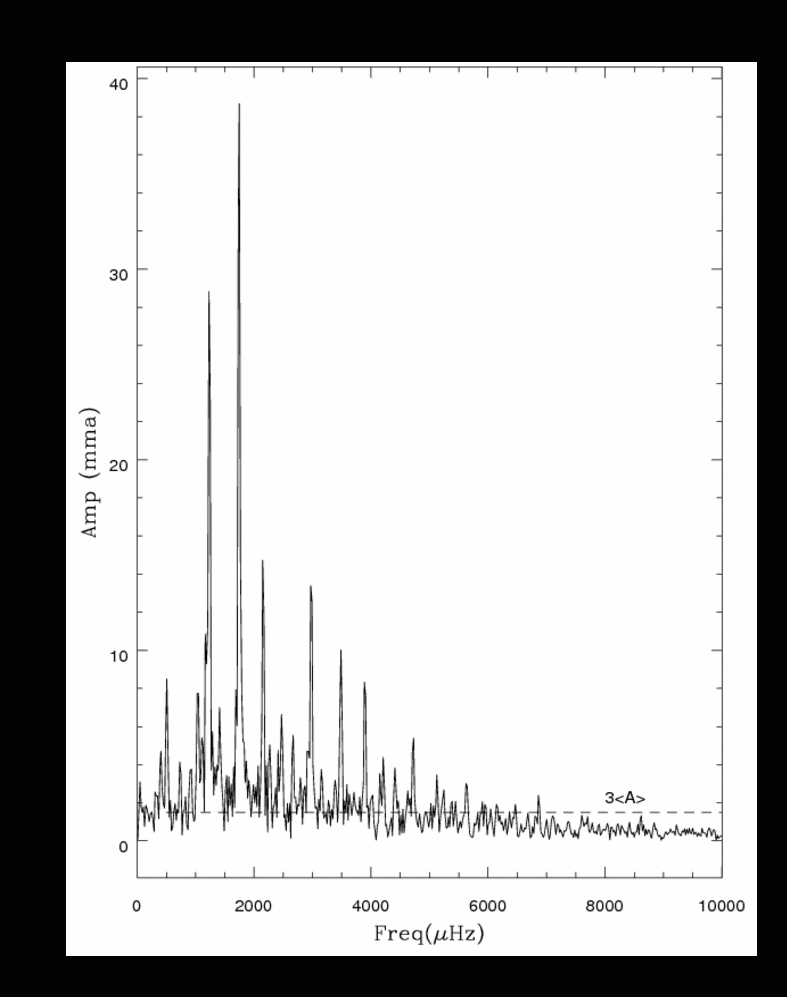
O espectro de potências 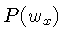 é definido como:
é definido como:
e o ângulo de fase (relacionado a quando o sinal é máximo) é dado por:
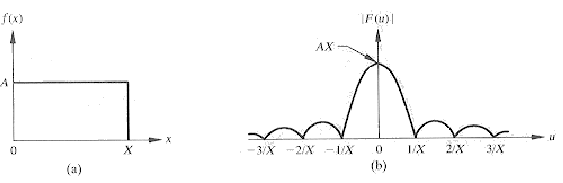
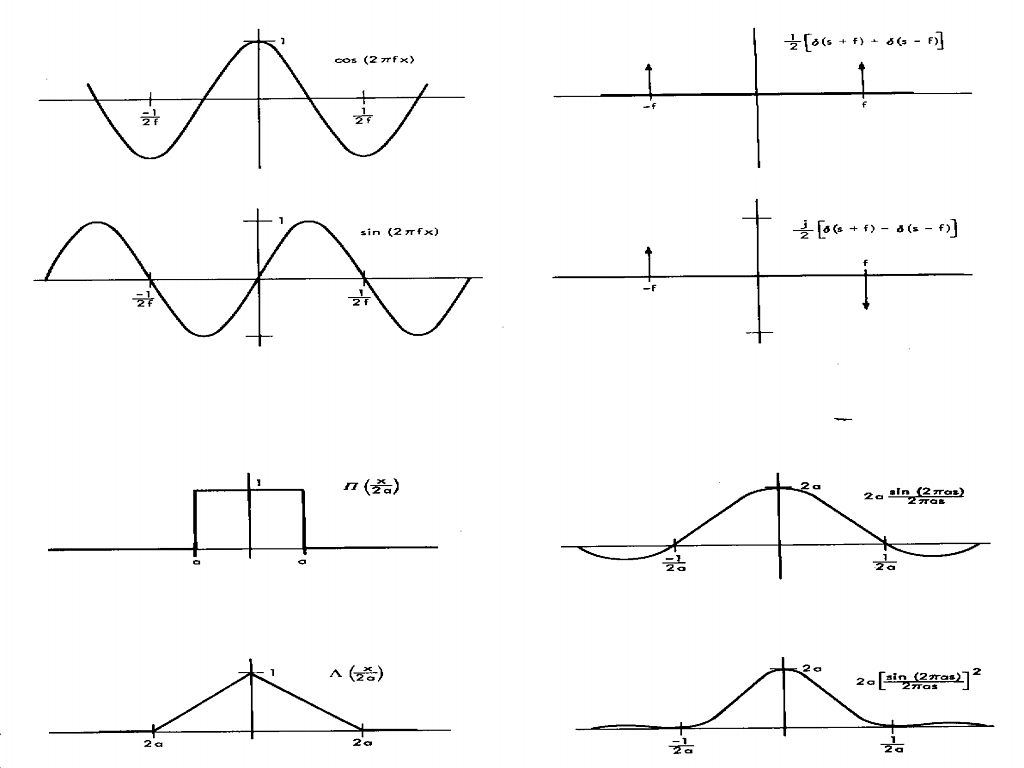
Por exemplo, podemos calcular a transformada de Fourier de um
pulso retangular, definido por:
A transformada de Fourier 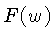 de
de 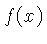 é dada por:
é dada por:
já que
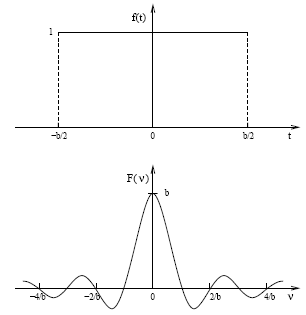
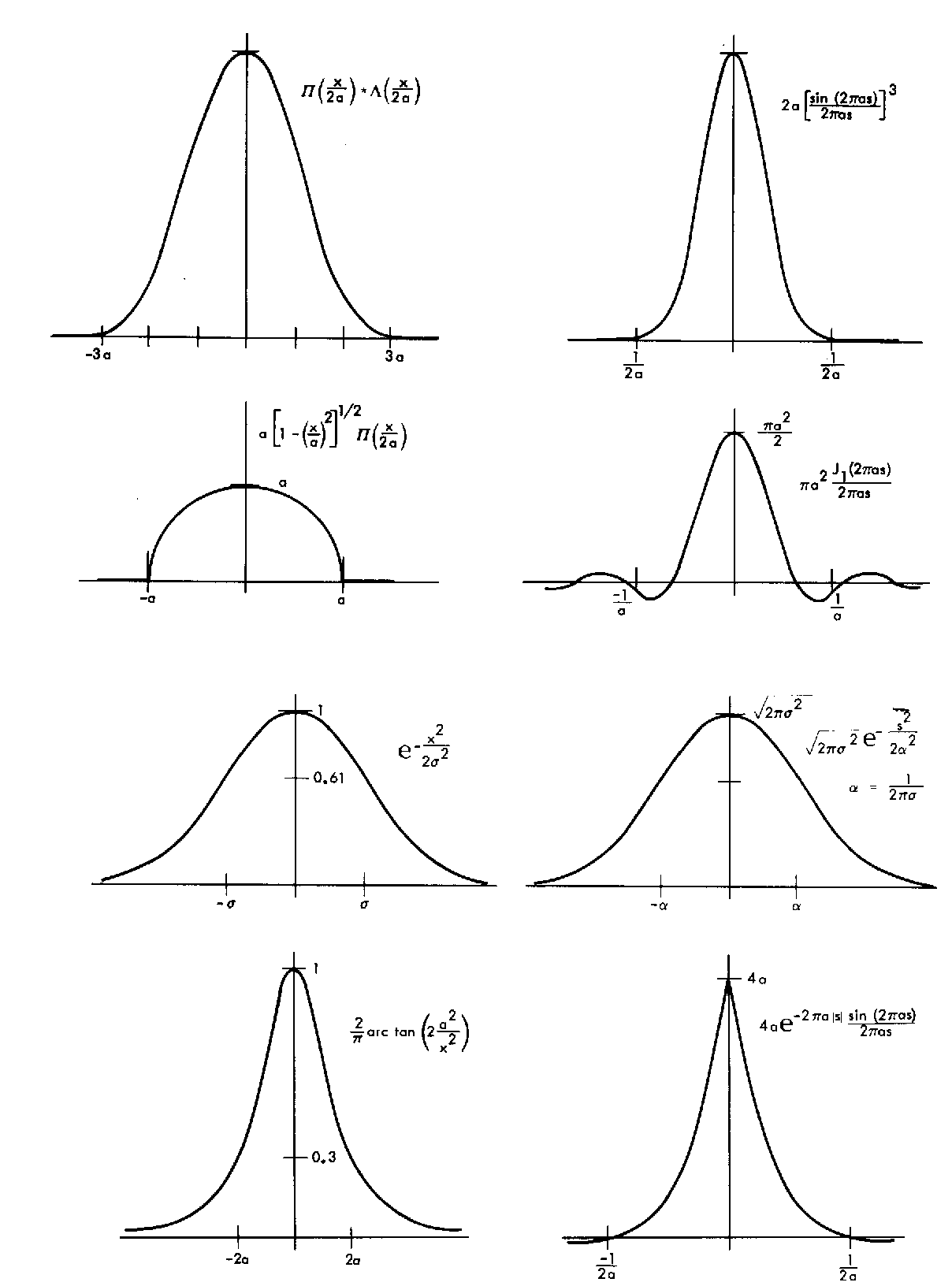
Transformada de Fourier de uma função caixa (um pulso retangular).
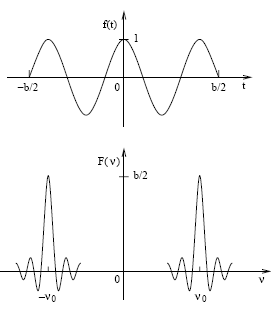
Transformada de Fourier de uma função coseno truncada, isto é, amostrada por um tempo finito.
O engenheiro americano Claude Elwood Shannon
(1916-2001), considerado o pai da teoria
da informação, demonstrou claramente o teorema de amostragem de
Nyquist-Shannon, baseado na proposta do engenheiro sueco Harry
Nyquist (1889-1976), provando que um sinal precisa ser amostrado
pelo menos duas vezes a cada ciclo para conter toda a informação
(1949, Proceedings of the Institute of Radio Engineers
37, 10).
Programa de Transformada

 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 28 jun 2011


![${\cal{F}}[f(x)] \equiv F(w_x) = \int_{-\infty}^\infty
f(x) e^{-2i\pi w_xx} dx$](img195.gif)
![${\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty
F(w_x) e^{2i\pi w_xx} dw_x$](img196.gif)
![]() , integramos a função
, integramos a função
![]() sobre todos os valores da coordenada
sobre todos os valores da coordenada
![]() . Se o valor da integral for grande para
esta freqüência, então o sinal tem uma componente significativa
nesta freqüência, isto é, uma parte significativa deste
sinal é composto por esta freqüência.
. Se o valor da integral for grande para
esta freqüência, então o sinal tem uma componente significativa
nesta freqüência, isto é, uma parte significativa deste
sinal é composto por esta freqüência.
![$ \boxed{{\cal{F}}[f(x)] \equiv F(\nu) = \int_{-\infty}^\infty f(x) e^{-i \nu x} dx,}$](img201.gif)
![$ \boxed{{\cal{F}}^{-1}[F(\nu)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(\nu) e^{i\nu x} d\nu,}$](img202.gif)
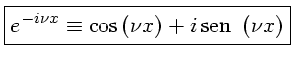
![]() qualquer é que a função seja
integrável, e finita, isto é:
qualquer é que a função seja
integrável, e finita, isto é:
![$ \boxed{F(w_x) = \Re[F(w_x)] + i\Im[F(w_x)].}$](img207.gif)
![]() é definido como:
é definido como:
![$ \boxed{P(w_x) = \Re[F(w_x)]^2 + \Im[F(w_x)]^2,}$](img209.gif)
![$ \boxed{\phi(w_x)=\tan^{-1} \frac {\Im[F(w_x)]}{\Re[F(w_x)]}.}$](img210.gif)
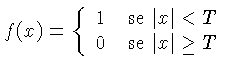
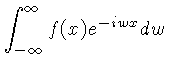
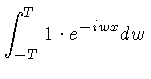
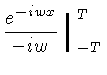
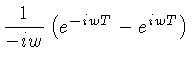
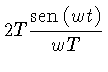
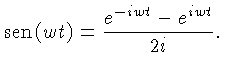


![]()