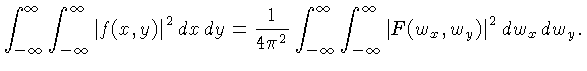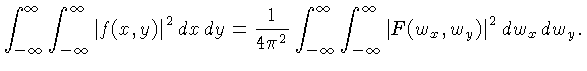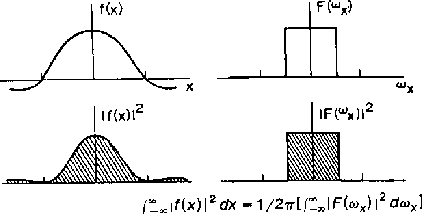Próxima: Transformada de Derivadas Volta: Transformadas de Fourier Anterior: Teorema da Convolução

Teorema de Parseval

A energia no domínio espacial e de Fourier estão relacionadas pela integral do quadrado do sinal sobre todo o domínio:

$$\int_{-\infty}^\infty \int_{-\infty}^\infty \left\vert f(x,y)\rig... ...ty}^\infty \int_{-\infty}^\infty \left\vert F(w_x,w_y)\right\vert^2 dw_x\,dw_y.$$

Ou seja, a energia total no domínio espacial é a mesma no domínio de Fourier.

Próxima: Transformada de Derivadas Volta: Transformadas de Fourier Anterior: Teorema da Convolução