



Próxima: Amostragem
Volta: Transformadas de Fourier
Anterior: Teorema de Parseval
Transformada de Derivadas
A transformada de uma derivada da função é dada por:
já que, pela definição da transformada inversa:
de modo que:
que é a transformada inversa de
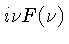 .
.
Em duas dimensões:
e a transformada da derivada segunda de uma função, ou Laplaciano,
é dada por:




Próxima: Amostragem
Volta: Transformadas de Fourier
Anterior: Teorema de Parseval
©
Modificada em 21 set 1998
![$\displaystyle {\cal{F}}\left[\frac{df(x)}{dx}\right]=i\nu F(\nu),$](img308.gif)
![$\displaystyle {\cal{F}}\left[\frac{df(x)}{dx}\right]=i\nu F(\nu),$](img308.gif)
![$\displaystyle {\cal{F}}^{-1}\left[F(\nu)\right]=f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}
F(\nu)e^{i\nu x}\,d\nu,$](img309.gif)
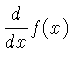
![$\displaystyle \frac{1}{2\pi} \frac{d}{dx} \left[\int_{-\infty}^{\infty}
F(\nu)e^{i\nu x}\,d\nu\right]$](img311.gif)
![$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\nu) \frac{\partial}{\partial x}\left[e^{i\nu x}\right]\,d\nu$](img312.gif)
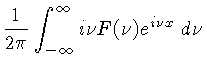
![$\displaystyle {\cal{F}}\left[\frac{\partial f(x,y)}{\partial x} +\frac{\partial...
...,y)}{\partial y} \right]=
i\left(\nu_x + \nu_y\right)F\left(\nu_x,\nu_y\right),$](img315.gif)
![$\displaystyle {\cal{F}}\left[\frac{\partial^2 f(x,y)}{\partial x^2} +\frac{\par...
...partial y^2} \right]=
-\left(\nu_x^2 + \nu_y^2\right)F\left(\nu_x,\nu_y\right).$](img316.gif)