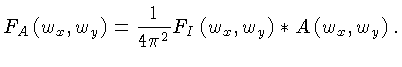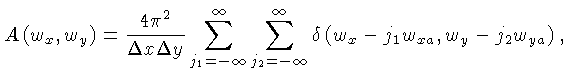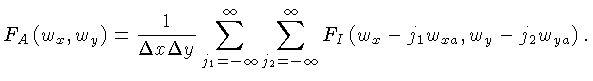Próxima: Alias
Volta: Transformadas de Fourier
Anterior: Transformada de Derivadas
Amostragem
Vamos chamar de 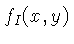 uma imagem ideal. Para medí-la,
multiplicamos esta imagem no domínio espacial por uma
função de amostragem, consistindo de uma série de
funções delta, como uma ''cama de pregos'':
onde
uma imagem ideal. Para medí-la,
multiplicamos esta imagem no domínio espacial por uma
função de amostragem, consistindo de uma série de
funções delta, como uma ''cama de pregos'':
onde 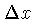 e
e 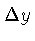 representam os espaçamentos,
e
representam os espaçamentos,
e 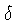 a função delta de Dirac. A função
depois de amostrada é dada por:
A transformada de Fourier da função amostrada é dada por:
De acordo com o Teorema da Convolução, a transformada
de Fourier pode ser expressa como a convolução da
transformada de duas funções,
a função delta de Dirac. A função
depois de amostrada é dada por:
A transformada de Fourier da função amostrada é dada por:
De acordo com o Teorema da Convolução, a transformada
de Fourier pode ser expressa como a convolução da
transformada de duas funções,
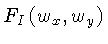 ,
e da função de amostra
,
e da função de amostra
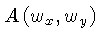 :
Como a transformada de Fourier de uma série infinita de funções
delta é uma série infinita de funções delta no domínio
de frequências:
onde
:
Como a transformada de Fourier de uma série infinita de funções
delta é uma série infinita de funções delta no domínio
de frequências:
onde
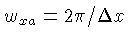 e
e
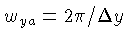 representam a frequência de amostragem no espaço
de Fourier. Como a convolução de uma função
com a função delta é a própria função,
podemos reescrever:
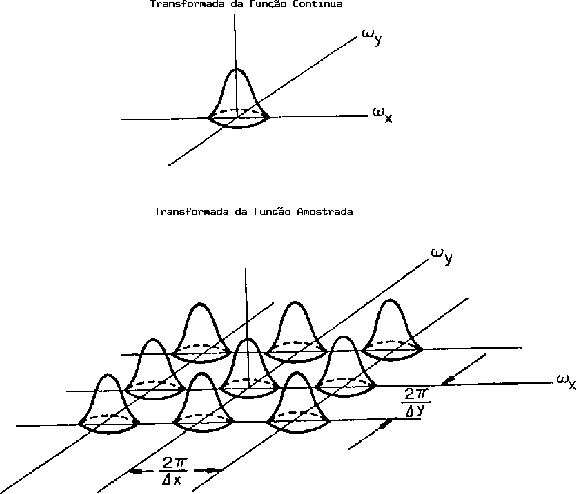
Esta equação representa a réplica da transformada
representam a frequência de amostragem no espaço
de Fourier. Como a convolução de uma função
com a função delta é a própria função,
podemos reescrever:
Esta equação representa a réplica da transformada
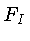 da função original
da função original 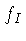 no espaço de Fourier,
com separações
no espaço de Fourier,
com separações
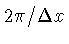 e
e
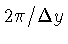 .
.




Próxima: Alias
Volta: Transformadas de Fourier
Anterior: Transformada de Derivadas
©
Modificada em 21 set 1998
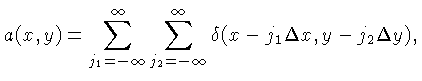
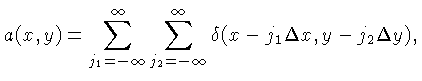
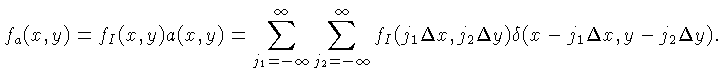
![$\displaystyle F_a\left(w_x,w_y\right)=\int_{-\infty}^\infty \int_{-\infty}^\infty
f_a(x,y)\exp\left[-i\left(w_xx+w_yy\right)\right]dx\,dy.$](img322.gif)