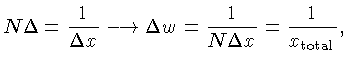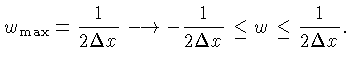Próxima: Transformada de Hankel
Volta: Transformadas de Fourier
Anterior: Amostragem
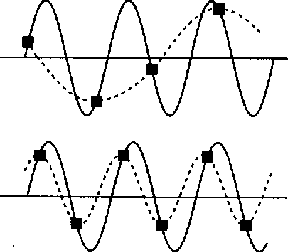
Alias
Para obter a reconstrução da imagem, é preciso que esta
imagem tenha sido amostrada na frequência de Nyquist ou superior.
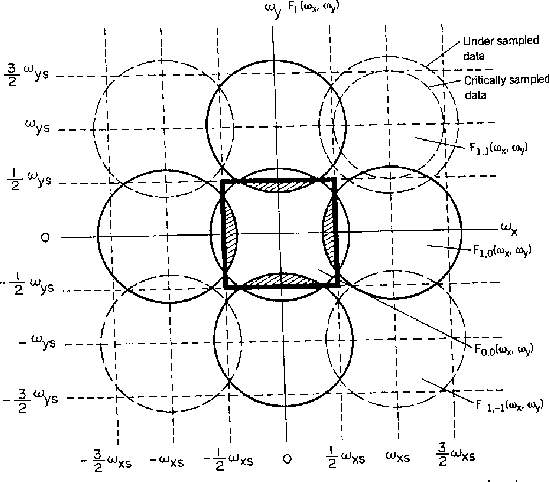
Se a imagem for amostrada em um frequência inferior,
haverá perda de informação e
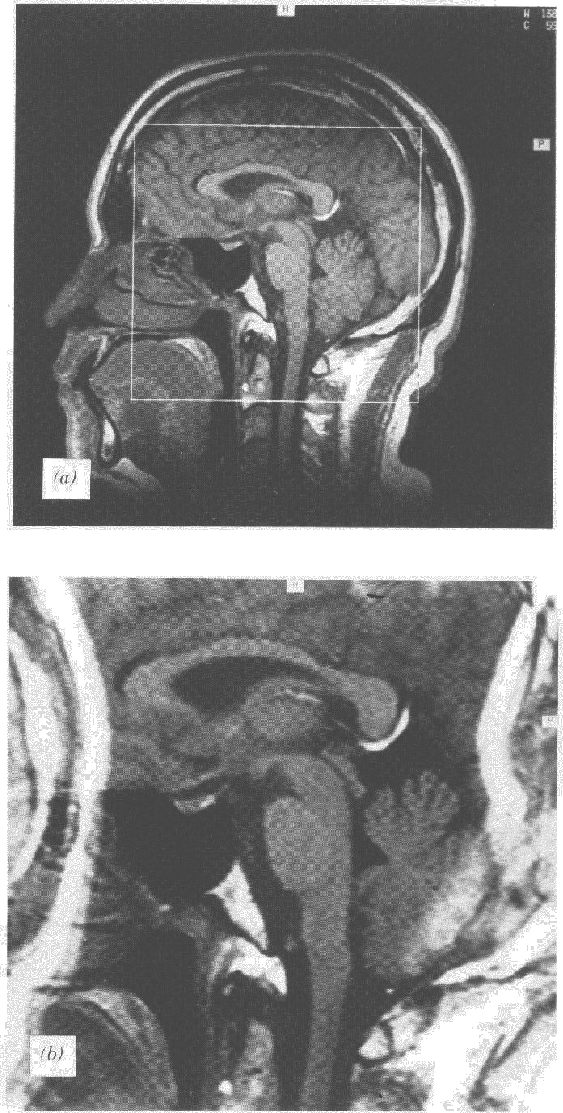
a superposição da transformada de Fourier causará o
alias, como nesta imagem de ressonância nuclear magnética:
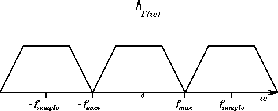
Se o sinal consiste de N medidas independentes, devemos calcular a transformada
de Fourier em um total de N pontos de frequência. Se calcularmos
menos pontos, não usaremos toda a informação. Se calcularmos mais
pontos, teremos redundâncias. Devemos portanto calcular N pontos
espaçados de  , onde
, onde
e




Próxima: Transformada de Hankel
Volta: Transformadas de Fourier
Anterior: Amostragem
©
Modificada em 21 set 1998


![]() , onde
, onde