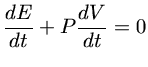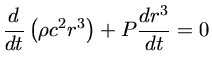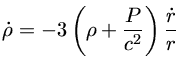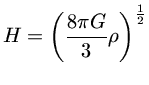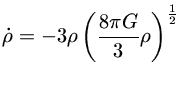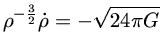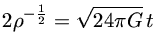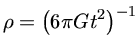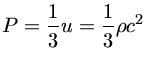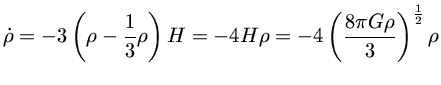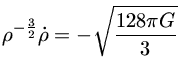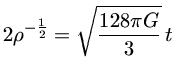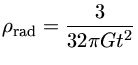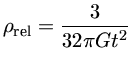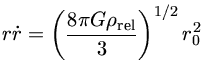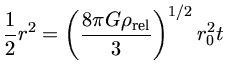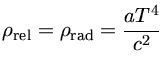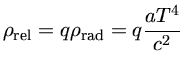Consideremos a conservação de energia para um volume V;
a primeira lei da termodinâmica pode ser escrita como:
onde 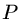 é a pressão e
é a pressão e 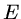 é a densidade de matéria-energia no
volume
é a densidade de matéria-energia no
volume 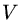 ,
,
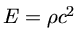 . Considerando
. Considerando
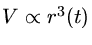 ,
ou seja,
de modo que
Identificando
,
ou seja,
de modo que
Identificando 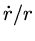 como a constante de Hubble,
obtemos
como a constante de Hubble,
obtemos
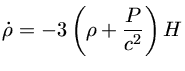
(1)
Se assumirmos um Universo dominado por matéria mas
que as partículas de matéria não interagem entre si, 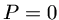 ,
Para uma geometria plana e constante cosmológica nula, já deduzimos que a constante de Hubble
será dada por
de modo que
ou seja
que pode ser integrado em relação ao tempo
ou seja,
para um Universo dominado por matéria mas com pressão nula.
,
Para uma geometria plana e constante cosmológica nula, já deduzimos que a constante de Hubble
será dada por
de modo que
ou seja
que pode ser integrado em relação ao tempo
ou seja,
para um Universo dominado por matéria mas com pressão nula.
Para um Universo dominado por radiação,
a equação (1) se transforma em
de modo que
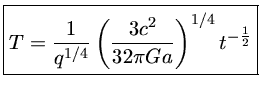
que pode ser integrado em relação ao tempo
ou seja,
No início do Universo ele era dominado pela radiação e esta radiação era
térmica, de modo que, independente de se o Universo é fechado ou aberto, a
densidade de massa das partículas relativísticas (fótons, neutrinos,
grávitons, ...) seguia a relação:
já que a equação de campo de Einstein, para pequenos valores do raio do
Universo r,
pode ser escrita como
que, com as condições iniciais r=0 em t=0, resulta em
para os primeiros instantes.
Se os fótons fossem os únicos componentes relativísticos de massa-energia presentes,
poderíamos escrever
onde 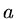 é a constante de densidade de radiação de Stefan-Boltzmann,
já que a densidade de energia para um corpo negro de temperatura T
é dada por
é a constante de densidade de radiação de Stefan-Boltzmann,
já que a densidade de energia para um corpo negro de temperatura T
é dada por 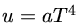 , e como
, e como 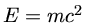 ,
,
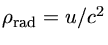 .
A densidade atual de energia em forma de radiação é diretamente
obtida usando-se a temperatura da radiação cósmica do fundo do Universo,
atualmente 2,73 K, obtendo-se
.
A densidade atual de energia em forma de radiação é diretamente
obtida usando-se a temperatura da radiação cósmica do fundo do Universo,
atualmente 2,73 K, obtendo-se
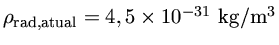 . Esta densidade é muito menor que a densidade
de matéria luminosa,
. Esta densidade é muito menor que a densidade
de matéria luminosa,
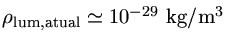 , de modo que vivemos em um Universo
dominado pela matéria.
, de modo que vivemos em um Universo
dominado pela matéria.
Entretanto, a altas temperaturas, a produção de pares de partículas-antipartículas
ocorre. Se escrevermos então que
onde 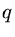 é um número inteiro maior do que um dependente da temperatura,
já que a produção de pares depende da temperatura, podemos escrever
Esta equação nos diz que
é um número inteiro maior do que um dependente da temperatura,
já que a produção de pares depende da temperatura, podemos escrever
Esta equação nos diz que
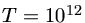 K(
K(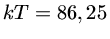 MeV) para t=
MeV) para t=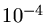 s e
s e
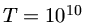 K (
K (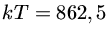 keV) para t=1 s e
keV) para t=1 s e
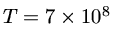 K (
K (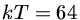 keV) para t=180 s.
Comparando com a energia de repouso (
keV) para t=180 s.
Comparando com a energia de repouso (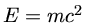 ) do próton, de 931 MeV,
e do eletron, de 511 keV, vemos que para t<2μs a
destruição de pares de bárions-antibárions está em equilíbrio termodinâmico
com a radiação ambiente, e para t< 0,7s, pares elétron-pósitrons
estavam em equilíbrio com a radiação.
) do próton, de 931 MeV,
e do eletron, de 511 keV, vemos que para t<2μs a
destruição de pares de bárions-antibárions está em equilíbrio termodinâmico
com a radiação ambiente, e para t< 0,7s, pares elétron-pósitrons
estavam em equilíbrio com a radiação.


Próxima: Efeitos da Constante Cosmológica
Volta: Cosmologia Relativística
Anterior: Levantando e Baixando Índices
Volta: Astronomia e Astrofisica
©
Modificada em 18 jun 2008