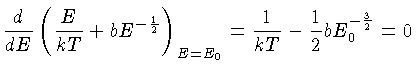Próxima: Reações Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Seção de Choque e Taxa de
O raio de um núcleo de massa atômica 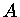 pode ser representado
por
pode ser representado
por
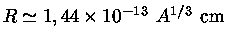 |
(1.69f) |
Para uma reação 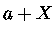 ,
,
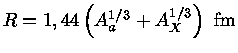 |
(1.69g) |
onde fm é um fentometro, também chamado de um fermi,
e corresponde a 10-13 cm.
Para que uma reação nuclear ocorra, as partículas
precisam vencer a barreira Coulombiana
[Charles Augustin de Coulomb (1736-1806)]
repulsiva entre as
partículas, dada por
enquanto que a energia cinética entre as partículas
é determinada por uma distribuição de velocidades de
Maxwell-Boltzmann correspondente à energia térmica
Para temperaturas da ordem de dezenas a centenas de milhões
de graus, a energia média das partículas
interagentes são
muitas ordens de magnitudes menores
do que a barreira Coulombiana que as separa.
As reações ocorrem pelo efeito de tunelamento quântico, proposto em 1928
pelo físico russo-americano George Antonovich Gamow (1904-1968).
As partículas
com maior chance de penetrar a barreira são aquelas com
a máxima energia na distribuição de Maxwell-Boltzmann:
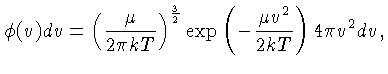 |
(1.70) |
onde 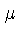 é a massa reduzida das partículas
é a massa reduzida das partículas 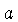 e
e 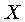 .
Entretanto, a distribuição de Maxwell-Boltzmann mostra
que o
número de pares de partículas com energia
muito acima de
.
Entretanto, a distribuição de Maxwell-Boltzmann mostra
que o
número de pares de partículas com energia
muito acima de 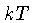 decresce rapidamente com a energia.
George Gamow foi o primeiro a demonstrar que a probabilidade
de duas partículas de carga
decresce rapidamente com a energia.
George Gamow foi o primeiro a demonstrar que a probabilidade
de duas partículas de carga 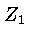 e
e 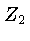 , movendo-se
com velocidade relativa
, movendo-se
com velocidade relativa 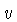 ,
penetrar sua repulsão
eletrostática é proporcional ao fator
,
penetrar sua repulsão
eletrostática é proporcional ao fator
Penetração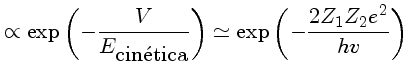 |
(1.71) |
já que
pelo Princípio da Incerteza
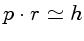 .
.
 As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
Penetração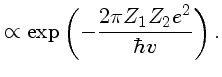 |
(1.71a) |
Considerando níveis de energia espaçados pelo comprimento de onda de de Broglie,
a interação entre duas partículas também
é proporcional ao fator quantum-geométrico (seção
de choque, cross-section)
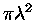 ,
onde
,
onde 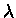 é o comprimento de onda de de Broglie:
é o comprimento de onda de de Broglie:
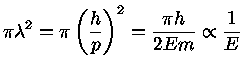 |
(1.72) |
Para um parâmetro de aproximação (distância mínima)
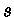 , o momentum angular quantizado é
, o momentum angular quantizado é
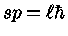 , e a seção
de choque passando de um estado
, e a seção
de choque passando de um estado 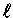 para
para 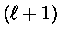 é dada
pela diferença de área equivalente à zona de interação
é dada
pela diferença de área equivalente à zona de interação
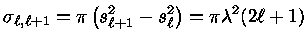 |
(1.72a) |
Para dois núcleos tunelarem pela barreira de Coulomb, sua separação deve ser menor ou da ordem do comprimento de de Broglie,
para que suas funções de onda se sobreponham.
Gamow mostrou que, para r ≤ λdB,
que para o ciclo p-p, a energia de Gamow equivale a EG=0,49 MeV, e para um par de α, EG=31,3 MeV.
Para uma energia térmica do núcleo do Sol E≃2 keV, a probabilidade de tunelamento, ou penetração, para próton-próton é e-15,7≃10-7.
Vamos escrever energia de Gamow como EG≡ 1/√b.
Em baixa energia, tanto (1.71) quanto (1.72)
variam rapidamente com a energia.
Com essas motivações,
definimos a seção de choque a baixas energias como
um produto de três fatores dependentes da energia:
onde
e
A
é o peso atômico reduzido
O fator S(E)
representa a parte nuclear da probabilidade de ocorrência
da reação, enquanto os outros dois fatores representam
dependências não-nucleares, bem conhecidas.
O fator S(E)
é normalmente constante ou fracamente dependente da energia
sobre uma faixa limitada de energias, se a reação é não ressonante. Tem dimensão de energia vezes área, e é frequentemente
dado em unidades de keV barn=1,60×10-33 ergs cm2.
Este fator foi definido por Edwin Salpeter (1924-2008) em 1952.
A distribuição de velocidades de Maxwell-Boltzmann pode ser
escrita em termos da distribuição de energia:
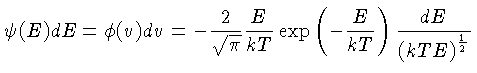 |
(1.74) |
e
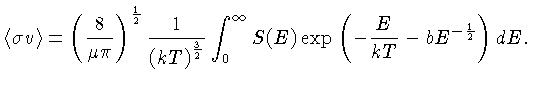 |
(1.75) |
O fator
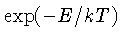 decresce para altas energias, enquanto que o fator
decresce para altas energias, enquanto que o fator
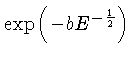 decresce para baixas energias.
As reações são mais efetivas para uma energia
decresce para baixas energias.
As reações são mais efetivas para uma energia 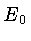 determinada
pelo máximo do integrando:
ou
determinada
pelo máximo do integrando:
ou
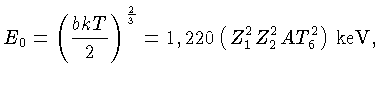 |
(1.76) |
onde
T6
é a temperatura em milhões de graus Kelvin, e
E0
é chamada de energia efetiva para a reação nuclear.
Pela equação (1.76),
podemos calcular que
a energia efetiva para a reação nuclear para partículas
leves e temperaturas de algumas dezenas de milhões de graus,
obtendo E0≃10
a 30 keV, enquanto que a energia térmica
é de
kT = 0,086T6 keV, refletindo o fato que a penetração
da barreira Coulombiana favorece as partículas de alta energia
da distribuição de Maxwell-Boltzmann.





Próxima: Reações Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Seção de Choque e Taxa de
©
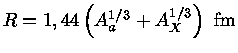

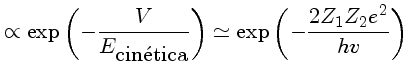
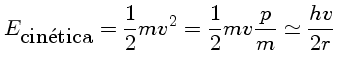
 As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
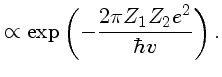



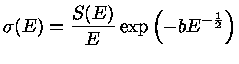
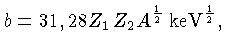
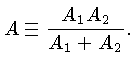
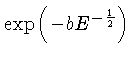 decresce para baixas energias.
As reações são mais efetivas para uma energia
decresce para baixas energias.
As reações são mais efetivas para uma energia