




Próxima:
Escudamento Eletrônico
Volta: Geração de Energia Nuclear
Anterior: Reações Não-Ressonantes
Em 1936, o russo
Gregory Breit (1899-1981) e o húngaro Eugene Paul Wigner
(Jenó Pál Wigner, 1902-1995), publicaram (Physical Review, 49, 519)
a fórmula de Breit-Wigner para um nível único,
que descreve a parte ressonante da seção de choque para
um estado com
largura natural 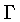 :
que tem a forma de uma lorentziana.
:
que tem a forma de uma lorentziana.
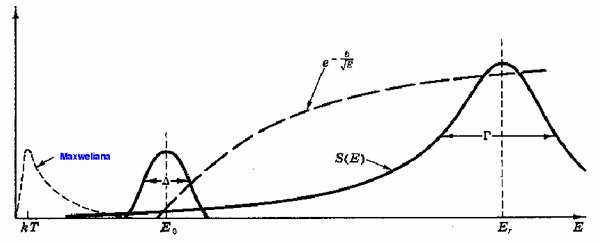
Portanto, para reações ressonantes, a função S(E)
varia muito com a energia, e tem a forma:
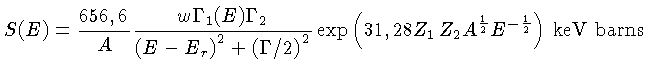 |
(1.77) |
onde
e 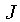 é o momentum angular da ressonância e
é o momentum angular da ressonância e 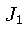 e
e 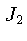 são os spins das partículas 1 e 2, e 1 barn=
são os spins das partículas 1 e 2, e 1 barn=
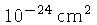 .
.
Fatores dominantes na taxa de reação nuclear.
|
As taxas de reações nucleares estão disponíveis na internet em
http://www.nucastrodata.org e
http://www.phy.ornl.gov/astrophysics/data/data.html, e foram publicadas
principalmente por
Georgeanne Robertson Caughlan (1916-1994)
e William Alfred Fowler (1911-1995)
em 1988
( Atomic Data and Nuclear Data Tables, 40, 283). William Fowler recebeu
o prêmio Nobel em física em 1983, por seus estudos de
reações nucleares e a formação dos elementos no Universo.
Uma lista mais moderna foi publicada em 1999 por Carmen Angulo Pérez
(1965-) e
colaboradores [C. Angulo et al., (1999), Nuclear Physics, A656, 3-187]
do NACRE e está disponível em
http://pntpm.ulb.ac.be/Nacre/nacre.htm.
Para o ciclo p-p, a primeira reação
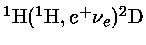 é não-ressonante, e
a maior incerteza é o tempo de vida média
do nêutron para decaimento β,
da ordem de
15 min (885,7 ± 0,8 s),
necessário para
calcular-se o processo inverso de decaimento do próton.
A dependência em energia dessa reação é
diretamente dependente da barreira coulombiana entre os dois
prótons, e:
é não-ressonante, e
a maior incerteza é o tempo de vida média
do nêutron para decaimento β,
da ordem de
15 min (885,7 ± 0,8 s),
necessário para
calcular-se o processo inverso de decaimento do próton.
A dependência em energia dessa reação é
diretamente dependente da barreira coulombiana entre os dois
prótons, e:
A taxa de reação é obtida multiplicando-se por 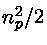 ,
onde o fator de 1/2 porque não podemos contar as partículas
idênticas duas vezes.
,
onde o fator de 1/2 porque não podemos contar as partículas
idênticas duas vezes.
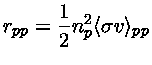 |
(1) |
A vida média de um próton em relação à sua
destruição pela reação p+p é dada por
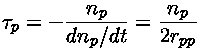 |
(2) |
Para
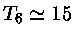 ,
,
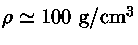 e
e
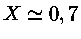 ,
obtemos
,
obtemos
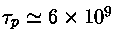 anos;
a reação p+p é
tão lenta que efetivamente controla a velocidade com a qual o
ciclo próton-próton opera.
anos;
a reação p+p é
tão lenta que efetivamente controla a velocidade com a qual o
ciclo próton-próton opera.
A quantidade de reações em cada um dos três ramos do ciclo PP,
PPI, PPII e PPIII, depende da temperatura, e é ascendente, isto é,
para baixas temperaturas o PPI domina e, para altas temperaturas, o
PPIII domina. Para temperaturas de
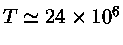 K,
as cadeias PPII e PPIII contribuem igualmente. A reação
final do PPIII, que é o decaimento do
K,
as cadeias PPII e PPIII contribuem igualmente. A reação
final do PPIII, que é o decaimento do
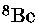 em duas partículas-
em duas partículas-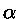 ocorre também, em processo
inverso, na queima do hélio pelo triplo-
ocorre também, em processo
inverso, na queima do hélio pelo triplo-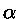 . O núcleo
de
. O núcleo
de
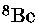 é extremamente instável, decaindo em
é extremamente instável, decaindo em
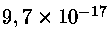 s.
s.
A energia térmica liberada pelo ciclo p-p também depende da cadeia,
e um valor efetivo de 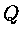 pode ser estimado levando-se em conta
os pesos relativos:
pode ser estimado levando-se em conta
os pesos relativos:
![$ Q_{ef} = 13,116 [ 1 + 1,412\times 10^8 (1/X-1)e^{-4,998/T_9^{1/3}}]~{MeV}$](taxa/img20.gif) |
(3) |
e a geração de energia por unidade de massa é dada por:
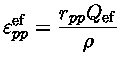 |
(4) |
Usando somente os primeiros termos, obtemos como primeira
aproximação
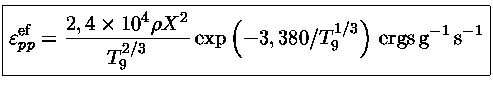 |
(5) |
O deutério é queimado mesmo em baixa temperatura (
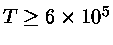 K)
e, portanto, qualquer deutério primordial é queimado já na fase de pré-seqüência principal.
K)
e, portanto, qualquer deutério primordial é queimado já na fase de pré-seqüência principal.
No ciclo CNO, se a temperatura for alta o suficiente, o principal
núcleo resultante, entre C, O e N, será o
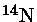 ,
e praticamente todo o
,
e praticamente todo o
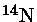 da natureza foi formado dessa
maneira.
da natureza foi formado dessa
maneira.
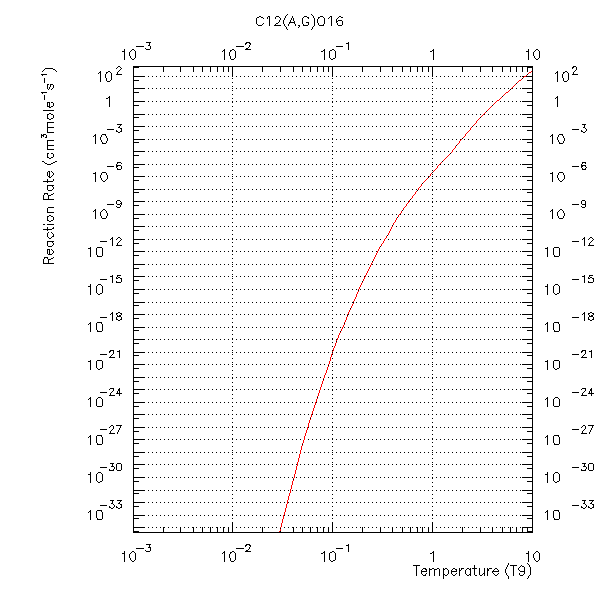
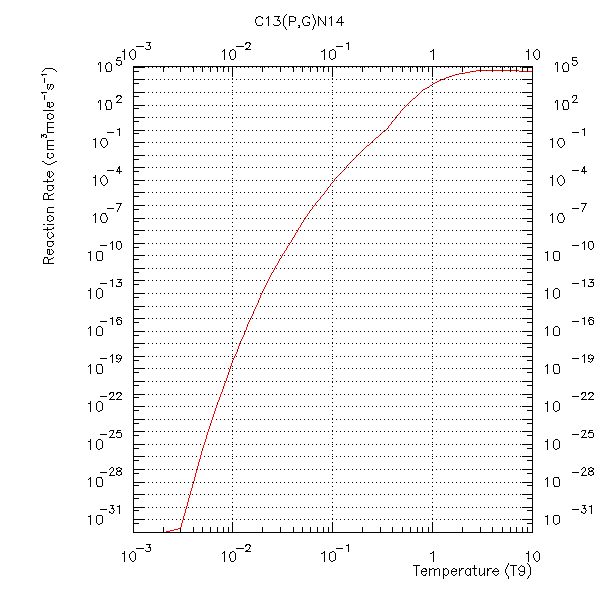
Taxa de reação nuclear para
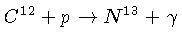
e
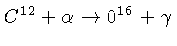
.
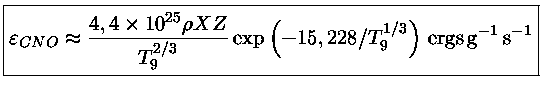 |
(6) |
Para uma temperatura central como a solar de
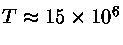 K,
X=0,7 e Z=0,02,
K,
X=0,7 e Z=0,02,
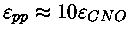 , de modo
que a contribuição do ciclo CNO para a geração de energia
total no Sol é de 10%. Mas estrelas um pouco mais massivas do que o
Sol têm temperatura central suficientemente mais alta para o
ciclo CNO dominar.
, de modo
que a contribuição do ciclo CNO para a geração de energia
total no Sol é de 10%. Mas estrelas um pouco mais massivas do que o
Sol têm temperatura central suficientemente mais alta para o
ciclo CNO dominar.
Valores centrais de produção de energia termonuclear
e pressão, para X=0,74 e Y=0,24.
| M |
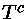 |
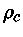 |
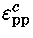 |
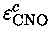 |
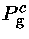 |
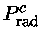 |
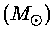 |
(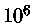 K) K) |
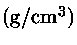 |
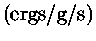 |
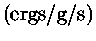 |
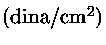 |
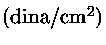 |
|
1 |
14,42 |
82,2 |
16,98 |
0,61 |
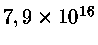 |
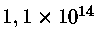 |
|
1,2 |
16,67 |
85,7 |
30,95 |
11,04 |
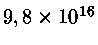 |
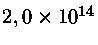 |
|
2 |
21,09 |
47,0 |
39,36 |
463,63 |
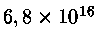 |
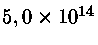 |
O artigo de Antonio Caciolli e colaboradores do LUNA
(2011, Revision of
the 15N(p,γ)16O reaction rate and oxygen abundance
in H-burning zones)
propõe que a taxa é 50% menor do que tabelada pelo NACRE.
Esta nova taxa levou à redução da idade dos aglomerados por 1 Gano
(Aldo Serenelli, 2014, AIP Conference Proceedings, 1594, 137).
Já para a queima do hélio pelo ciclo triplo-
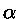 ,
,
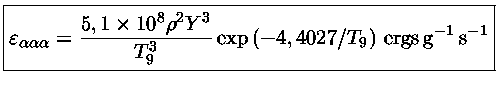 |
(7) |
Para
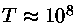 K,
K,
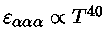 ,
consideravelmente mais alto do que para a queima do hidrogênio e,
portanto, potencialmente mais explosivo.
,
consideravelmente mais alto do que para a queima do hidrogênio e,
portanto, potencialmente mais explosivo.
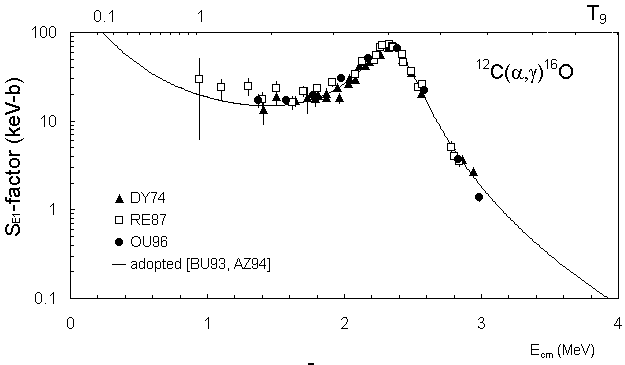
A próxima reação importante é a captura de uma partícula
α
pelo
12C formando um 16O.
Essa reação
se dá próxima a uma ressonância, causando uma incerteza de uma
fator de dois, experimental e teórica, na seção de choque.
O valor utilizado atualmente para esta reação para as energias
estelares é resultado de uma extrapolação dos dados experimentais
por oito ordens de magnitude, de acordo com William Alfred Fowler [1986,
Highlights of Modern Physics, ed. Stuart Louis Shapiro (1947-) &
Saul A. Teukolski (1947-),
New York: John Wiley & Sons, p.3], obtendo
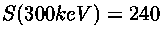 keV barns.
A incerteza nessa reação limita nosso conhecimento da composição do
núcleo das estrelas anãs brancas,
das estrelas no Ramo Gigante Assimptótico, e SNIa, provenientes de estrelas
da sequência principal com massa menor do que
8 a 10 M⊙ isto é,
da razão entre carbono e oxigênio.
Em 2001, Travis Scott Metcalfe (1973-) inferiu um valor de
keV barns.
A incerteza nessa reação limita nosso conhecimento da composição do
núcleo das estrelas anãs brancas,
das estrelas no Ramo Gigante Assimptótico, e SNIa, provenientes de estrelas
da sequência principal com massa menor do que
8 a 10 M⊙ isto é,
da razão entre carbono e oxigênio.
Em 2001, Travis Scott Metcalfe (1973-) inferiu um valor de
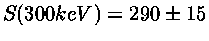 keV barns para a seção de
choque, utilizando a asterosismologia de anãs brancas pulsantes
para restringir a fração de oxigênio
keV barns para a seção de
choque, utilizando a asterosismologia de anãs brancas pulsantes
para restringir a fração de oxigênio
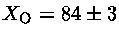 % para a DBV GD358, com
% para a DBV GD358, com
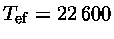 K e
K e
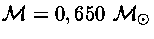 .
.
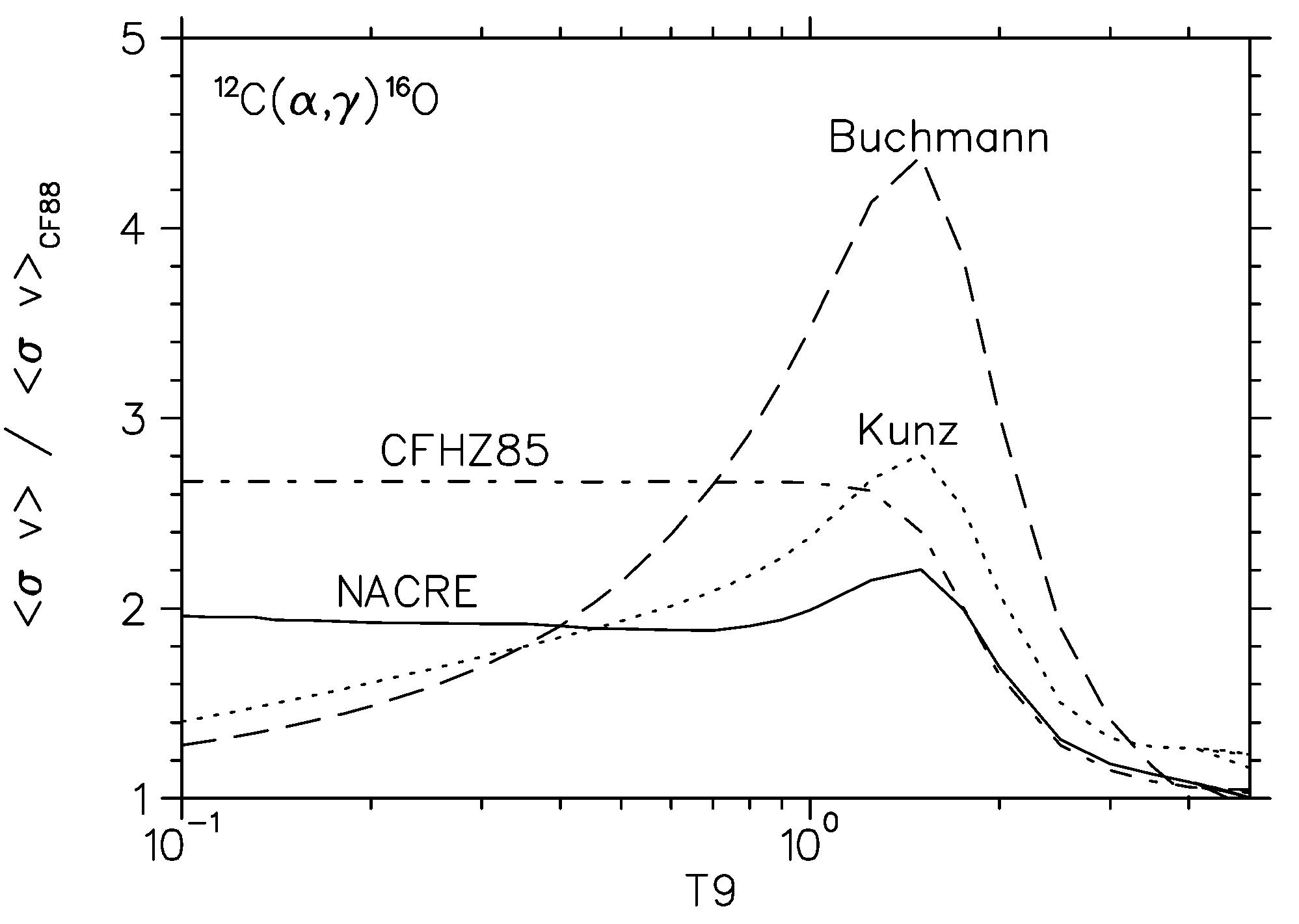
Mounib El Eid discute em dois artigos
(2004, Astrophysical Journal, 611, 452; 2005, Nature, 433, 117),
as incertezas na reação. O gráfico mostra a razão entre as secções de choques de diversas
determinações:
CFHZ85, de Caughlan, G. R., Fowler, W. A., Harris, M. J., & Zimmerman, B. A.
(1985, Atomic Data and Nuclear Data Tables, 32, 197);
CF88, de Caughlan, G. R. & Fowler, W. A.
(1988, Atomic Data and Nuclear Data Tables, 40, 283);
L. Buchmann
(1996, ApJ, 468, L127;
NACRE (Nuclear Astrophysics Compilation of REaction Rates) de Carmen Angulo et al.
(1999, Nuclear Physics A, 656, 3) e
R. Kunz et al.
(2002, ApJ, 567, 643).
Marlete
Pereira Meira de Assunção, da UNIFESP, e colaboradores do
Stuttgart DYNAMITRON accelerator
(2006, Physical Review C, 73, 5801),
publicaram uma nova determinação experimental,
entre 1,850 MeV e 3,730 MeV, da seção de choque.
Na região de energia que corresponde a janela de Gamow para a
queima do hélio, da ordem de 300 keV, a
seção de choque é da ordem de 10-41cm2,
com contribuições de captura radiativa E1 e E2 da mesma ordem.
Como medidas desta ordem são totalmente inatingíveis com as técnicas
experimentais atuais, medidas em outras energias para restringir a extrapolação
são necessárias.
A componente E1 tem ressonâncias em 2,424 e -0,045 MeV, em relação ao
centro de massa, e a componente E2 em 2,683 e -0.045 MeV, além de outras
de mais alta energia.
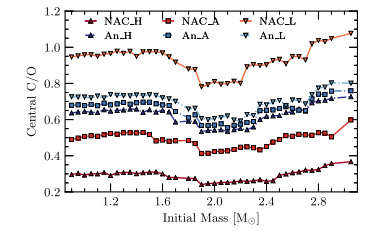
Ben Thomas Pepper, Aline G. Istrate, Alejandra Daniela Romero & S. O. Kepler
(2022, The impact of the uncertainties in the 12C(α,γ)16O reaction rate on the evolution of low- to intermediate-mass stars,
MNRAS, 513, 1499) calculam o efeito da incerteza na taxa de reação C(α,γ)O na razão C/O da composição do núcleo nos modelos de 0,95 a 3,05 M
⊙ na fase de anã branca.
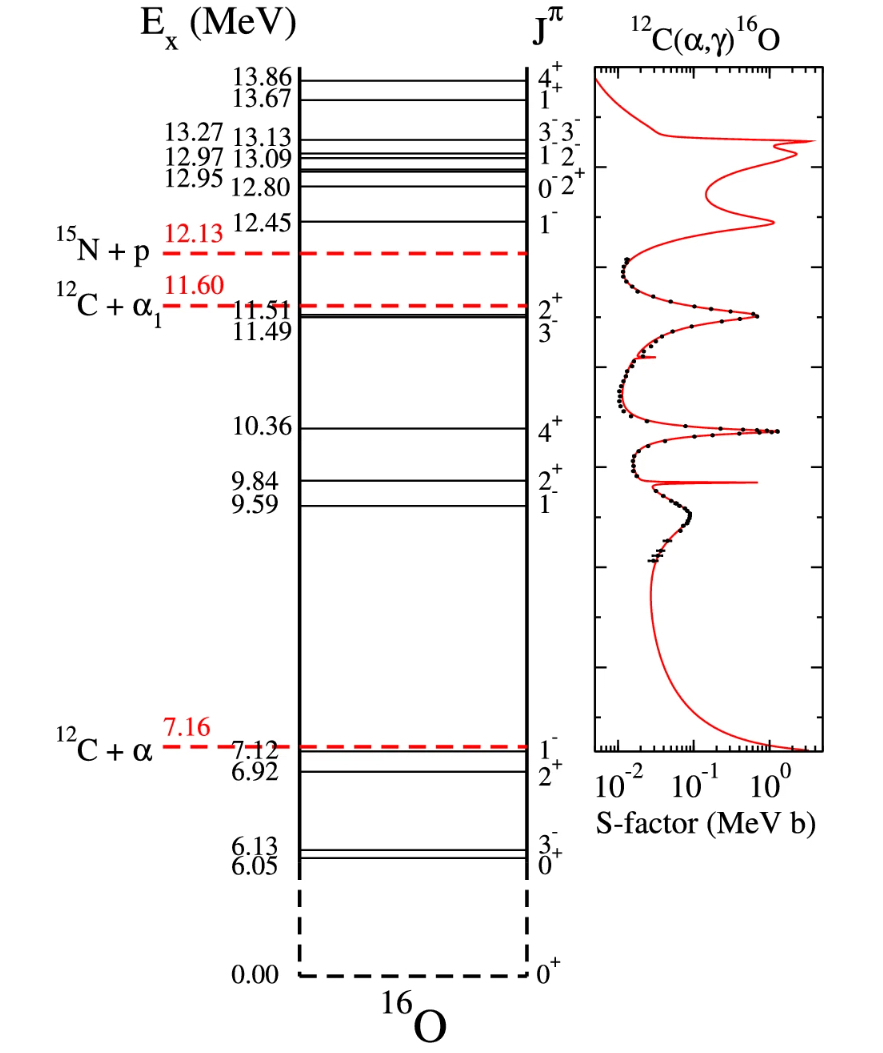 Richard James de Boer
Richard James de Boer
et al.
(2025,
The 12C(α,γ)16O reaction, in the laboratory and in the stars,
The European Physical Journal A, 61, 70)
mostra que embora dominate na queima do He, esta secção de choque para energia de Gamow da ordem de 300 keV é extremamente pequena, da ordem de σ=2×10
-17 barn,
o que torna os experimentos atuais insensíveis, de modo que o somente por extrapolação de experimentos a mais alta energia podemos estimá-la.
Michael Wiescher (2009, Physics, 2, 69) discute
a incerteza nas
abundâncias isotópicas produzidas pelo processo-s em uma
estrela de 25 massas solares, devido às incertezas
na seção de choque da reação 22Ne+α→n+25Mg,
que é uma grandes produtoras de nêutrons.
A vida média de um nêutron livre é 881,5±1,5 s (14 minutos, 42 segundos),
de modo que a meia-vida [que difere da vida média por ln(2) = 0,693] é 611,0±1,0 s (10 minutos, 11 segundos).
Vários artigos recentes apresentam redeterminações de secções de choque nucleares importantes na produção dos elementos nas estrelas:
L. Y. Zhang et al. (2021,
Thermonuclear 19F(p,sα)16O Reaction Rate Revised and Astrophysical Implications, ApJ, 913, 51Z),
Umberto Battino et al.
2023,
Impact of newly measured 26Al(n,p)26Mg and 26Al(n,α)23Na reaction rates on the nucleosynthesis of 26Al in stars, MNRAS, 520, 2436B),
L.H. Wang et al. (2023,
Measurement of the O18(α,γ)Ne22 Reaction Rate at JUNA and its Impact on Probing the Origin of SiC Grains,
Ph.Rv.L., 130, 2701W),
C. Marshall et al. (2023, New constraints on sodium production in globular clusters from the 23Na(3He,d)24Mg reaction, Ph.Rv.C.,107, 5806M).





Próxima:
Escudamento Eletrônico
Síntese de Elementos Pesados
Volta: Geração de Energia Nuclear
Anterior: Reações Não-Ressonantes
©
![\sigma(E)=\frac{\Gamma}{2\pi [\left(E-E_r)^2+(\Gamma/2)^2]}](img583.gif)
![\sigma(E)=\frac{\Gamma}{2\pi [\left(E-E_r)^2+(\Gamma/2)^2]}](img583.gif)
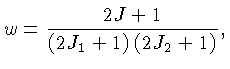
![]() é não-ressonante, e
a maior incerteza é o tempo de vida média
do nêutron para decaimento β,
da ordem de
15 min (885,7 ± 0,8 s),
necessário para
calcular-se o processo inverso de decaimento do próton.
A dependência em energia dessa reação é
diretamente dependente da barreira coulombiana entre os dois
prótons, e:
é não-ressonante, e
a maior incerteza é o tempo de vida média
do nêutron para decaimento β,
da ordem de
15 min (885,7 ± 0,8 s),
necessário para
calcular-se o processo inverso de decaimento do próton.
A dependência em energia dessa reação é
diretamente dependente da barreira coulombiana entre os dois
prótons, e:
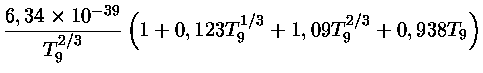
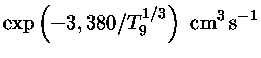
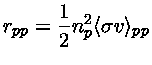
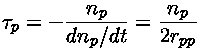
![]() K,
as cadeias PPII e PPIII contribuem igualmente. A reação
final do PPIII, que é o decaimento do
K,
as cadeias PPII e PPIII contribuem igualmente. A reação
final do PPIII, que é o decaimento do
![]() em duas partículas-
em duas partículas-![]() ocorre também, em processo
inverso, na queima do hélio pelo triplo-
ocorre também, em processo
inverso, na queima do hélio pelo triplo-![]() . O núcleo
de
. O núcleo
de
![]() é extremamente instável, decaindo em
é extremamente instável, decaindo em
![]() s.
s.
![]() pode ser estimado levando-se em conta
os pesos relativos:
pode ser estimado levando-se em conta
os pesos relativos:
![$ Q_{ef} = 13,116 [ 1 + 1,412\times 10^8 (1/X-1)e^{-4,998/T_9^{1/3}}]~{MeV}$](taxa/img20.gif)
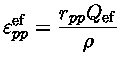
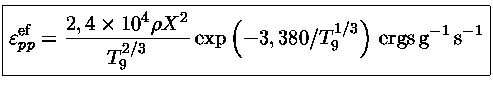
![]() ,
e praticamente todo o
,
e praticamente todo o
![]() da natureza foi formado dessa
maneira.
da natureza foi formado dessa
maneira.


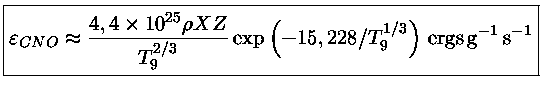
![]() ,
,
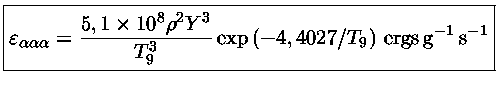
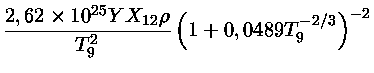
![$ \exp{[-32,12T_9^{-1/3}-(0,286 T_9)^2]}~{ergs\,g^{-1}\,s^{-1}}$](taxa/img57.gif)


