| Estrelas de Nêutrons |
Multiplicando (1.102) por 4π r2, podemos integrá-la, resultando em:
onde Mr denota a massa gravitacional dentro de r: de modo que para r=R, Mr=M, a massa gravitacional da estrela. Esta é a massa que um observador distante mede por efeitos gravitacionais, como por exemplo, efeitos orbitais. Ela não é entretanto a massa relacionada com o número de bárions simplesmente, pois contém também toda a energia, dividida por c2. Desta forma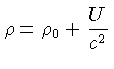
Diferenciando a equação (1.100) em relação a r, obtemos P′ em função de (λ, λ′,ν′,ν′′, r). Podemos eliminar λ, λ′,ν′,ν′′ utilizando as equações (1.100), (1.101) e (1.102), chegando à equação de Tolman-Oppenheimer-Volkoff para o equilíbrio hidrostático na relatividade geral:
Esta equação, derivada em 1939 por Richard Chase Tolman (1881-1948), Julius Robert Oppenheimer (1904-1967) e George Michael Volkoff (1914-2000), se reverte à forma usual da Equação do Equilíbrio Hidrostático (1.24) para c2 → ∞. A expressão relativística para o gradiente de pressão (dP/eλ/2 dr) é maior do que no caso Newtoniano (dP/dr), de modo que a pressão no interior da estrela aumenta mais rapidamente.
De acordo com George William Collins II (1937-2013)
[1989, The Fundamentals of Stellar Astrophysics, (New York: Freeman)],
um modelo simples é
![]() .
A equação da continuidade da massa
.
A equação da continuidade da massa
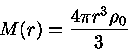
![\frac{dP(r)}{dr}= -\frac{4\pi Gr\rho_0^2[1+P/(\rho_0 c^2)][1+3P/(\rho_0 c^2)]} {3[1-8\pi G\rho_0 r^2/(3c^2)]}](relat/img4.gif)
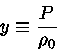
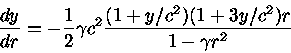
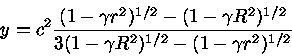
![P(r)=\rho_0 c^2 \frac{[1-2GMr^2/(R^3c^2)]^{1/2} -[1-2GM/(Rc^2)]^{1/2}} {3[1-2GM/(Rc^2)]^{1/2} -[1-2GMr^2/(R^3c^2)]^{1/2}}](relat/img10.gif)
![P_c=\rho_0 c^2 \frac{1-[1-2GM/(Rc^2)]^{1/2}} {3[1-2GM/(Rc^2)]^{1/2}-1}](relat/img11.gif)
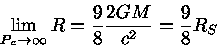
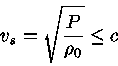
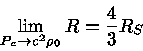

A verdadeira equação de estado das estrelas de nêutrons ainda não é conhecida, já que não sabemos como descrever a força forte, mas Edwin Salpeter (1925-2008) (1961, Astrophysical Journal, 134, 669) mostrou que, para um gás de elétrons e núcleos atômicos de peso atômico A e carga Z, com μo=A/Z, incluindo os efeitos Coulombianos da rede de íons, as correções de Thomas-Fermi [Llewellyn H. Thomas (1903-1992), 1927, The calculation of atomic fields, Proceedings of the Cambridge Philosophical Society, 23, 542-548; Enrico Fermi (1901-1954), 1927, Un metodo statistice per la determinazione di alcune proprieta del l'atomo. Rendiconti Accademia Nazionale dei Lincei, 6, 602-607] para a não uniformidade da distribuição de elétrons (escudamento eletrônico), energia de troca e interações spin-spin dos elétrons, podemos escrever a equação de forma paramétrica como
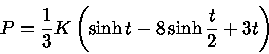
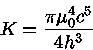
![t=4\log{\frac{\hat{p}}{\mu_0 c}+[1+(\frac{\hat{p}}{\mu_0 c})^2]^{1/2}}](relat/img21.gif)
Subrahmanyan Chandrasekhar (1910-1995) e Robert Forest Tooper (-2013) (1964, Astrophysical Journal, 183, 941) demontraram que as anãs brancas colapsam por efeitos da relatividade geral com 98% da massa de Chandrasekhar. Para as estrelas de nêutrons, a relatividade geral causa o colapso muito antes de toda a estrela tornar-se relativisticamente degenerada.
Nas estrelas de nêutrons, os elétrons degenerados têm energia suficiente para induzir o decaimento β inverso, isto é, colidir com um próton formando um nêutron. O subsequente decaimento β não é possível porque implicaria na emissão de um próton e um elétron de menor energia e, portanto, em um estado já completamente ocupado.
Desta maneira prótons são convertidos em nêutrons, formando núcleos ricos em nêutrons. Neste caso, a repulsão coulombiana é reduzida e núcleos mais pesados que o 56Fe são formados.
Podemos estimar a densidade média de uma estrela de nêutrons, considerando que a massa média é de 1,4 M⊙ e raio de 10 km
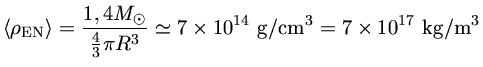
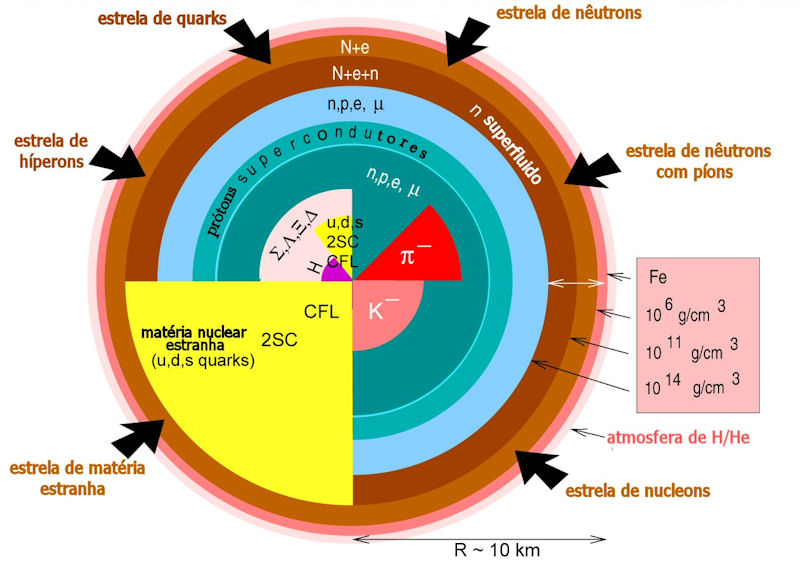
Para densidades superiores, os núcleos começam a se unir, formando um denso gás de elétrons, prótons e nêutrons. A equação de estado depende então fortemente da interação entre os núcleons, ainda incerta. Para densidades de 1018 kg/m3, píons, múons e híperons são energeticamente possíveis, e acima disto, os quarks tornam-se importantes. A coexistência em equilíbrio de nêutrons, prótons e elétrons, para temperatura desprezável, é caracterizada por
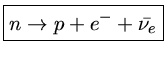 e
e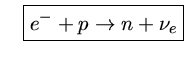
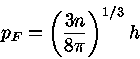
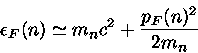
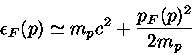
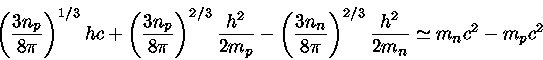
Para estrelas de nêutron, as densidades são maiores que
as da matéria nuclear.
Neste caso,
a Energia de Fermi é da ordem de
EF≃30 MeV, correspondendo
a
T=EF/k ≃3×1011 K. Portanto a energia cinética
devido a degenerescência é a principal contribuição
à pressão, com correções substanciais devido às forças
nucleares. A agitação térmica é desprezável,
já que a emissão de neutrinos no colapso para estrela de nêutrons
esfria o núcleo para
T≪3×1011 K em poucos segundos.
O processo mais eficiente de formação de neutrinos é o processo URCA
(![]() e
e
![]() ),
e Urca modificado
(
),
e Urca modificado
(![]() e
e
![]() ),
que é proporcial a T8, esfriando a estrela rapidamente para
T <1 09K.
Após algo entre 10 a 10 000 anos, o processo URCA torna-se
ineficiente, e esfriamento por bremsstrahlung de pares de neutrinos
e mais tarde por emissão térmica de fótons esfria a estrela e leva a
uma temperatura superficial de alguns milhões de Kelvin.
Mas se o núcleo não for composto por matéria normal, o esfriamento
pode ser mais complicado.
),
que é proporcial a T8, esfriando a estrela rapidamente para
T <1 09K.
Após algo entre 10 a 10 000 anos, o processo URCA torna-se
ineficiente, e esfriamento por bremsstrahlung de pares de neutrinos
e mais tarde por emissão térmica de fótons esfria a estrela e leva a
uma temperatura superficial de alguns milhões de Kelvin.
Mas se o núcleo não for composto por matéria normal, o esfriamento
pode ser mais complicado.
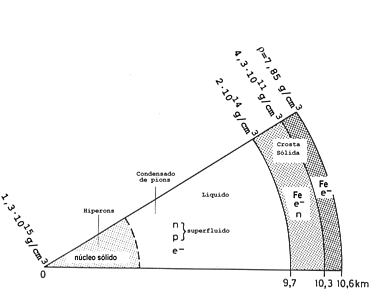
Desta forma, estranheza não é conservada em objetos astrofísicos. Nos núcleos atômicos estáveis, a massa dos híperons é maior do que a energia de Fermi, de modo que não é energeticamente favorável a transformação em híperons. As reações nucleares são tão rápidas τ≃10-22 s, que a estranheza é conservada nesta escala de tempo. Desta forma, embora a matéria nuclear normal tenha estranheza líquida zero, as estrelas de nêutrons podem ter, e quase certamente têm, híperons e ter estranheza líquida não nula (Norman K. Glendenning, 1997, Compact Stars, Springer: New York.)
A primeira derivação do colapso de uma estrela para o estágio de buraco negro foi publicada por Julius Robert Oppenheimer (1904-1967) e Hartland Snyder (1913-1962) (1939, Physical Review, 56), demonstrando que o último estágio do colapso é um buraco negro, e que a estrela corta qualquer comunicação com o exterior. Em 1974 o físico inglês Stephen William Hawking (1942-2018) demonstra que os efeitos de tunelamento quântico levam à evaporação de qualquer buraco negro, em escalas de tempo suficientemente grandes. Para um tratamento adequado do assunto, veja o livro Compact Stars, do físico Norman K. Glendenning, publicado pela Springer em 1997, ou as notas de Edward Lewis Robinson (1945-), Black Holes, que deduz o espaço-tempo de Kerr [Roy P. Kerr (1934-)] fora de um buraco negro em rotação (1963, Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics, Physics Review Letters, 11, 237), em coordenadas de Boyer-Lindquist [Robert H. Boyer & Richard W. Lindquist, Maximal Analytic Extension of the Kerr Metric, Journal Mathematical Physics, 8, 265, 1967], uma generalização da métrica de Schwarzschild.
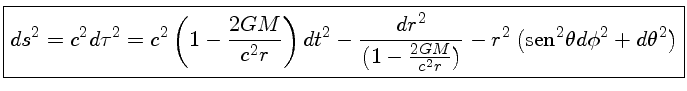 |
(Schwarzschild) |
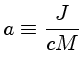
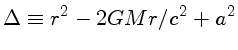
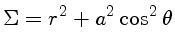
O tensor energia-momentum consiste do tensor do gás ideal adicionado ao tensor eletromagnetico.
Kuantay Boshkayev, Jorge A. Rueda, Remo Ruffini & Ivan Siutsou (2013, On General Relativistic Uniformly Rotating White Dwarfs,
Astrophysical Journal, 762, 117),
calcularam o limite de 1,467 M⊙ e período
de rotação máximo de 0,7 s, para uma anã
branca de oxigênio.
Pablo Marchant, Andreas Reisenegger, Juan Alejandro Valdivia & Jaime H. Hoys
(2014, Stability of Hall Equilibria in Neutron Stars, arXiv 1410.5833v1),
explicam que
na crosta das estrelas de nêutrons, os íons estão presos numa estrutura cristalina, e
somente os elétrons estão livres. Eles estudam o efeito da estrutura do campo magnético
na dissipação deste por oscilações amortecidas, devido ao efeito Hall, descoberto em
1879 por Edwin Herbert Hall (1855-1938), em que cargas elétricas movendo-se em um campo magnético
perpendicular à corrente se curvam devido à força de Lorentz, acumulando-se na superfície e gerando
um campo elétrico que se opõe ao movimento,
e devido ao efeito Ohmico, de perda de energia pela resistência do material.
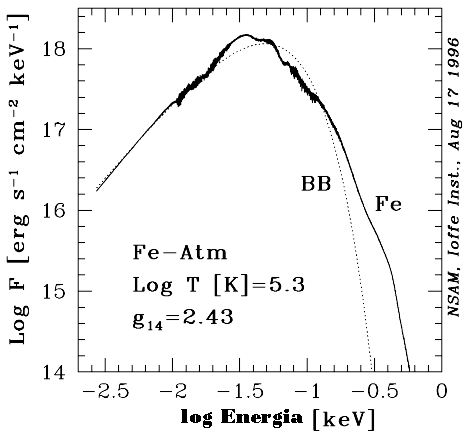
Sebastien Guillot e Robert E. Rutledge (2014, astroph 1409.4306v1) assumem que todas as estrelas de
nêutrons dentro de binárias de baixa massa quiecentes em raio-X (qLMXBs) têm o mesmo raio,
e ajustam o espectro térmico observado com um modelo com atmosfera de hidrogênio em
seis sistemas pertencentes a aglomerados globulares galácticos, obtendo
REN=9,4±1,2 km, o que os leva a restringir várias equações de
estado para a matéria nuclear.
A espessura da atmosfera da estrela de nêutrons pode ser estimada utilizando n(z)=n0e-z/H, com a escala de altura H=kT/mg, já que a há equilíbrio entre a força gravitacional e a pressão, kT. A escala de altura resultante é de apenas 0,13 cm, comparada com 8 km para a atmosfera da Terra. A densidade na atmosfera da estrela de nêutrons é 3,5 g/cm3, o que corresponde a carbono cristalino, de modo que a equação de estado não é de gás ideal.
Lukas R. Weih, Elias R. Most & Luciano Rezzolla, (2017, On the stability and maximum mass of differentially rotating relativistic stars, arXiv:1709.06058), obtiveram Mmax = (1,54 ± 0,05) MTOV, para todas as equações de estado que supuseram.
Equação de Estado para
o interior de estrelas de nêutrons, calculada por Alexander Yurievich Potekhin, do IOFFE.
Emanuele Berti, 2014, A Black Hole Primer