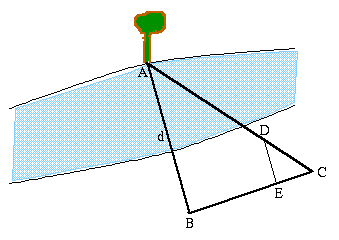
O método mais comum para se medir distâncias grandes, a pontos inacessíveis, é a triangulação [Tales de Mileto (c.624-546 a.C.)] - sabendo-se um dos lados de um sistema de triângulos e seus ângulos, podemos calcular todos os lados. Na figura abaixo está esquematizado, como exemplo, a maneira de medir a distância de uma árvore localizada do outro lado de um rio, sem atravessá-lo:

Tomando a árvore como um dos vértices, construímos os triângulos semelhantes ABC e DEC. BC é a linha de base do triângulo grande, AB e AC são os lados, que são as direções do objeto (a árvore) vistas de cada extremidade da linha base. Logo
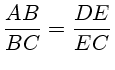
Como posso medir BC, DE e EC, posso calcular o lado AB e então, conhecer a distância da árvore.
Vemos que a direção da árvore, vista de B, é diferente da
direção da árvore vista de C. Esse deslocamento aparente na
direção do objeto observado devido à mudança de posição do
observador chama-se
paralaxe (do grego paralaxis, mudança).
Este é o princípio da
visão esteoroscópica do olho humano, que calcula a distância aos
objetos pela diferença de ângulo vista pelos dois olhos.
Quanto mais distante está o objeto, menor é a paralaxe.
Um aparelho profissional de medir ângulos é o teodolito.
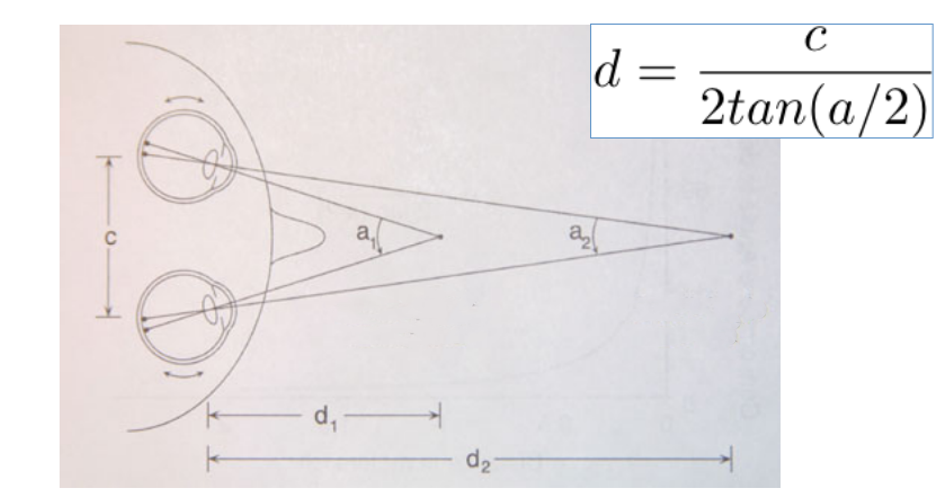
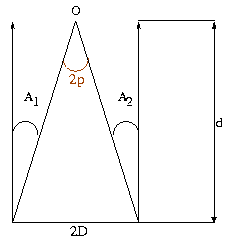
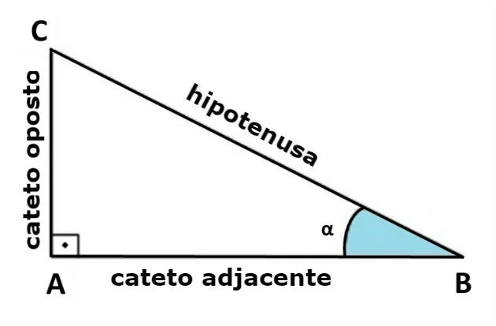
Pela trigonometria, sabemos que
Então, como a paralaxe das estrelas é menor do que 1 segundo de arco (1"=1°/3600):
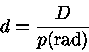
Para um triângulo de base D, altura d, diagonal B,
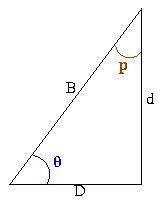
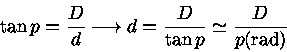
Transformação de graus em radianos
Em radianos, um ângulo é medido pelo arco que ele encerra, dividido pelo raio. Na figura abaixo, o arco de circunferência a corresponde ao ângulo α. Logo o valor de α em radianos é

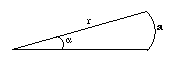
O valor, em graus, de 1 radiano, será:
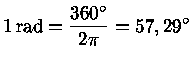

O mesmo método de triangulação explicado acima é usado para medir a distâncias de objetos astronômicos. Mas como esses objetos estão muito distantes, é necessário escolher uma linha de base muito grande. Para medir a distância da Lua ou dos planetas mais próximos, por exemplo, pode-se usar o diâmetro da Terra como linha de base. Para se medir a distância de estrelas próximas, usa-se o diâmetro da órbita da Terra como linha de base.
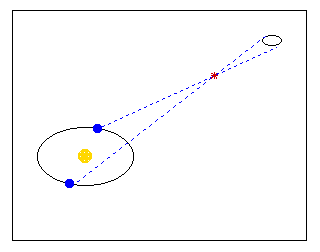
Atualmente a determinação de distâncias de planetas próximos é feita por radar, e não mais por triangulação, mas antes da invenção do radar, os astrônomos mediam as distâncias da Lua e de alguns planetas usando o diâmetro da Terra como linha de base. A figura abaixo ilustra o problema para a determinação da distância da Lua.
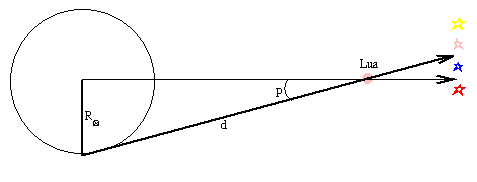
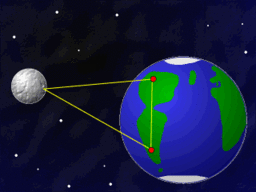


Se pudéssemos ver a Lua simultaneamente em 25 de abril de 2007,
de Porto Alegre (esquerda) e de Paris (direita), a veríamos
em posição diferente em relação às estrelas.
Hiparcos (c.190-c.120 a.C.) já sabia
que a paralaxe da Lua pode chegar a 1° (RTerra/distância Terra-Lua=6371 km/384 399 km=0,0166, e 0,0166 rad=57'), tendo calculado a distância mínima e máxima da Lua, e corrigia por isto
seus cálculos dos eclipses.
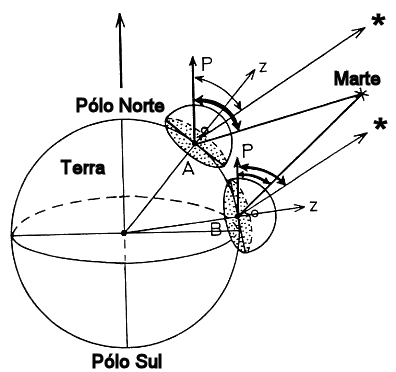
A posição da Lua em relação às estrelas distantes é medida duas vezes, em posições distantes na Terra, e a paralaxe corresponde à metade da variação total na direção observada dos dois lados opostos da Terra. Essa paralaxe é chamada paralaxe geocêntrica, e é expressa por:
![]()
para p sendo a paralaxe geoccêntrica.
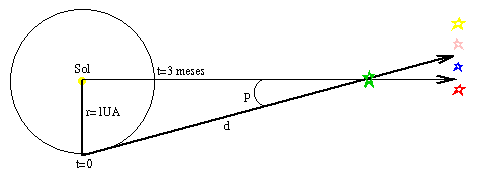
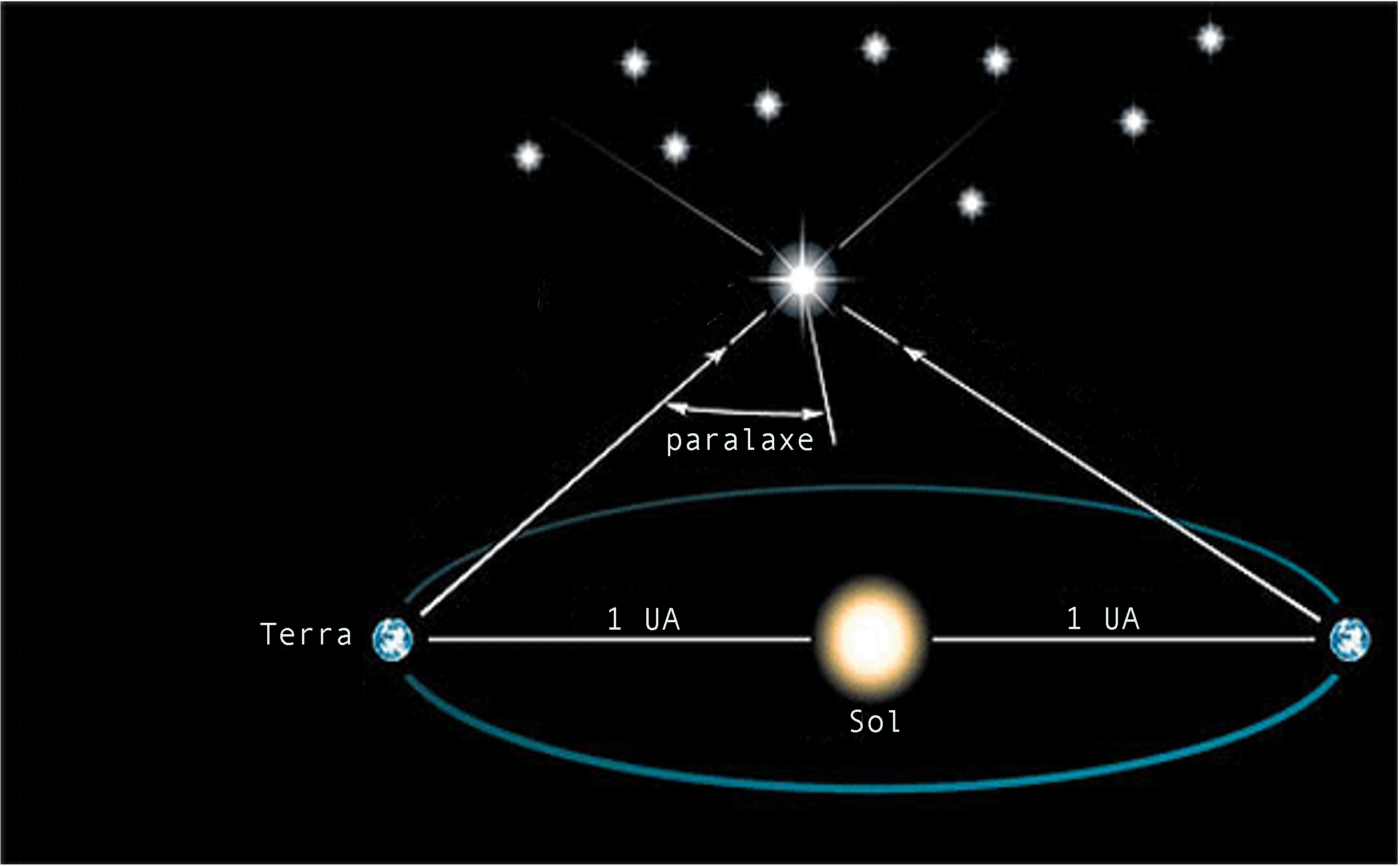
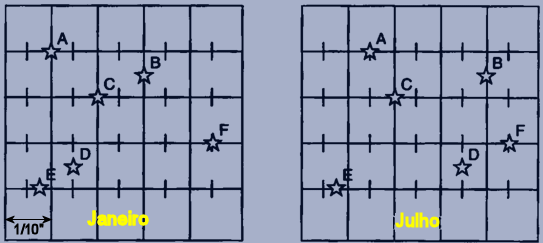
A paralaxe heliocêntrica é usada para medir a distância das estrelas mais próximas. À medida que a Terra gira em torno do Sol, podemos medir a direção de uma estrela em relação às estrelas de fundo quando a Terra está de um lado do Sol, e tornamos a fazer a medida seis meses mais tarde, quando a Terra está do outro lado do Sol. A metade do desvio total na posição da estrela corresponde à paralaxe heliocêntrica, que é expressa por:
![]()
para p sendo a paralaxe heliocêntrica.
 A primeira estimativa correta
do valor da Unidade Astronômica ocorreu
entre 5 de setembro e 1o de outubro de 1672,
quando o planeta Marte, com magnitude=-2,3, estava
muito próximo da
estrela brilhante ψ2 Aquarii
de magnitude=4,
e próximo da oposição de Marte, portanto
próximo do perigeu.
A primeira estimativa correta
do valor da Unidade Astronômica ocorreu
entre 5 de setembro e 1o de outubro de 1672,
quando o planeta Marte, com magnitude=-2,3, estava
muito próximo da
estrela brilhante ψ2 Aquarii
de magnitude=4,
e próximo da oposição de Marte, portanto
próximo do perigeu.
Com as observações simultâneas de Jean Richer (1630-1696) em Cayenne (5° N) na Guiana Francesa, Jean-Félix Picard (1620-1682) e pelo astrônomo dinamarquês Ole Christensen Rømer (1644-1710) em Paris, Giovanni Domenico Cassini (1625-1712) estimou a paralaxe de Marte como 15" entre Cayenne e Paris (7200 km de distância) e, considerando que Marte está a 1,52 UA do Sol, estimou o valor da UA como 140 milhões de km. O valor correto é de 149,597870691 milhões de km. Para comparação, o olho humano só consegue detectar ângulos maiores que cerca de 2'=2×60". A longitude de Cayenne não era conhecida com precisão, e os melhores relógios da época, pêndulos, não ficavam sincronziados durante as viagens marítimas, mas usando as luas de Júpiter, como proposto por Galileo, eles conseguiram sincronizar as observações.
A técnica mais precisa para determinar o comprimento da unidade astronômica
é por radar. No entanto, a determinação não pode ser feita diretamente,
pois se um sinal de rádio fosse emitido diretamente ao Sol, seu eco ficaria
perdido no meio de todos os sinais de rádio que o Sol emite. Portanto se usa
uma medida indireta. Por exemplo:
Suponha que um sinal de radar é enviado a Marte, quando este planeta está em
oposição, sendo encontrado que sua distância à Terra é 78 389 294 Km.
A distância média de Marte ao Sol é determinada pela terceira lei de
Kepler como sendo de 1,52 UA. A distância entre Terra e Marte, para Marte
em oposição, é portanto 0,52 UA.
Então
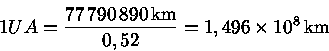
![]()
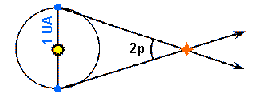

Determinação da velocidade da luz

A determinação da velocidade da luz foi feita pela primeira vez em 1675, pelo astrônomo dinamarquês Olaus Rømer (1644-1710), medindo o intervalo entre sucessivos eclipses da lua Io, de Júpiter (P=1,769138d), para diferentes pontos da órbita da Terra.
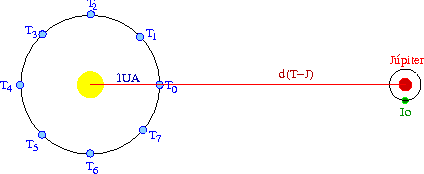
O intervalo de tempo entre os sucessivos eclipses é o período
de revolução do satélite, que pode
ser calculado pela 3a Lei de Kepler. Rømer verificou que os eclipses
ficavam atrasados quando Júpiter estava mais distante da Terra,
e adiantados quando Júpiter estava mais próximo da Terra.
O atraso total quando a Terra ia de ![]() para
para ![]() era de
1000 segundos. Rømer atribuiu o efeito ao tempo que a luz levava para
ir de um ponto da órbita da Terra ao outro, isto é, do tempo
que a luz levava para atravessar a diferença da distância
entre o satélite e a Terra.
era de
1000 segundos. Rømer atribuiu o efeito ao tempo que a luz levava para
ir de um ponto da órbita da Terra ao outro, isto é, do tempo
que a luz levava para atravessar a diferença da distância
entre o satélite e a Terra.
Para ficar mais claro, vamos considerar que ![]() é a hora
em que ocorre o eclipse quando a Terra está na posição
é a hora
em que ocorre o eclipse quando a Terra está na posição ![]() . Como
a luz tem velocidade finita, o eclipse só será visto na Terra
num tempo posterior, dado por:
. Como
a luz tem velocidade finita, o eclipse só será visto na Terra
num tempo posterior, dado por:
![]()
onde c é a velocidade da luz, e ![]() é a distância
entre a Terra e Júpiter na posição
é a distância
entre a Terra e Júpiter na posição ![]() .
.
Após um tempo ![]() , a Terra estará na posição
, a Terra estará na posição ![]() ,
e vamos chamar de
,
e vamos chamar de ![]() a hora prevista para acontecer o eclipse.
Mas na Terra, o eclipse só será observado em:
a hora prevista para acontecer o eclipse.
Mas na Terra, o eclipse só será observado em:
![]()
Logo, o intervalo de tempo observado entre os eclipses,
![]() , é maior do que o intervalo de tempo
real entre os eclipses,
, é maior do que o intervalo de tempo
real entre os eclipses, ![]() . A diferença
vai ser:
. A diferença
vai ser:
![]()
Se esta diferença é de 1000 s, então:
![]()
Como a
melhor estimativa para o eixo maior da órbita da Terra era 241 500 000 Km,
Rømer deduziu a velocidade da luz como sendo
![]()
A distância da Terra ao Sol foi medida em 1672, medindo-se a paralaxe de Marte em oposição, e sabendo-se que a distância a Marte é de 1,52 UA, como derivado por Copérnico. Hoje sabemos que o eixo maior da órbita da Terra é 2UA=299 795 786 Km, então a velocidade da luz é:
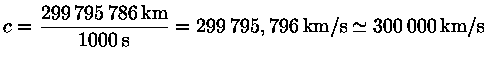
O ano-luz
O ano-luz (AL) é a distância percorrida pela luz em um ano. Essa distância equivale a:
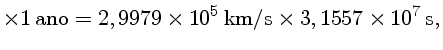
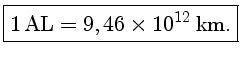
 >
>
1 Parsec é a distância de um objeto tal que, um observador nesse objeto veria o raio da órbita da Terra com um tamanho angular de 1′′, ou em outras palavras, é a distância de um objeto que apresenta paralaxe heliocêntrica de 1′′.
Como a distância em unidades astronômicas, corresponde a
![]()
e um ângulo de ![]() , expresso em radianos, vale
, expresso em radianos, vale
![]()
Logo:
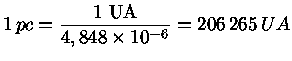
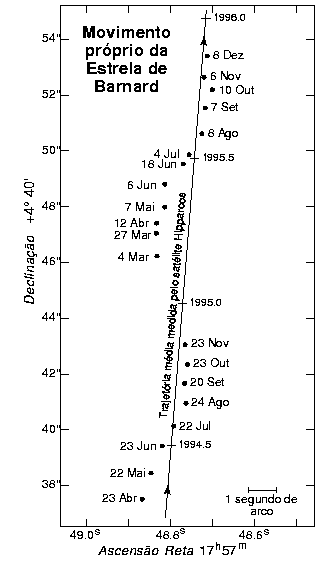
Embora proposta na antiguidade, a primeira medida exitosa de uma paralaxe estelar foi feita pelo matemático e astrônomo alemão Friedrich Wilhelm Bessel (1784-1846) em 1838, para a estrela binária visual 61 Cygni (AR=21h 06m 53.95s DEC=+38° 44′ 57.9′′, m=5,2), estimando p=0,31±0,1", correspondendo a uma distância de 600 mil UA = 10,4 anos-luz. O valor atual é 0,287±0,002". Ele escolheu esta estrela para observar porque notou que ela tinha um alto movimento próprio, de 5" por ano [Bessel, F. W. (1838). "On the parallax of 61 Cygni". Monthly Notices of the Royal Astronomical Society, 4: 152-161]. Apenas 35 estrelas conhecidas têm movimento próprio acima de 3" por ano. Edmond Haley (1656-1742) descobriu o movimento próprio das estrelas em 1718, comparando suas medidas da posição das estrelas com aquelas catalogadas por Ptolomeu, no Almagesto, já que a posição de Sírius havia mudado 30 minutos de arco no passar de 1800 anos. 30 minutos de arco é o diâmetro angular do Sol e da Lua. Em 1698, Christiaan Huygens (1629-1695) havia erroneamente estimado a distância de Sírius como 27 664 vezes a distância da Terra ao Sol, em seu livro Cosmotheoros, assumindo que o brilho de todas as estrelas deveria ser o mesmo. Gian Domenico Cassini (1625-1712), o astrônomo real inglês Nevil Maskelyne (1732-1811), Giuseppe Piazzi (1746-1826), o descobridor de Ceres, e o próprio Friedrich Wilhelm Bessel (1784-1846) haviam tentado medir a paralaxe de Sírius, sem sucesso.

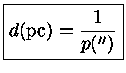
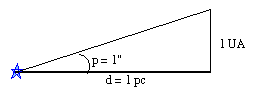
Resumindo as três unidades, para uma estrela com paralaxe heliocêntrica qualquer, sua distância será:
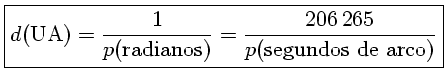
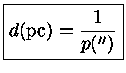
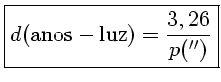
A estrela mais próxima da Terra, Próxima Centauri, está a uma distância de 4,3 AL, que é maior do que 1 pc (1,32 pc). Logo mesmo para a estrela mais próxima a paralaxe é menor do que 1′′ [na verdade é 0,7687±0,0003′′ (G. Fritz Benedict et al. 1999, Astronomical Journal, 118, 1086), usando o Telescópio Espacial Hubble].
 Até poucos anos, com os telescópios disponíveis na Terra,
a maior distância de estrelas que se podia medir com precisão melhor do que
10% era 20 pc, que corresponde a paralaxes ≤ 0,05′′
O uso de CCD e telescópios dedicados reduziu a incerteza das observações na Terra para até 1 mili-segundo de arco, similar à incerteza das medidas do
satélite HIPPARCOS (High-Precision Parallax Collecting Satellite),
construído para medir com alta
precisão a posição e a paralaxe
de 120 000 estrelas. Ele foi lançado em agosto de 1989 e operou
com sucesso por 3 anos, apesar de não ter alcançado a
órbita geoestacionária pretendida. É importante notar
que 1 mili-segundo de arco é equivalente
ao tamanho angular de uma pessoa na superfície da Lua vista da Terra.
Para atingir esta precisão, foi necessário corrigir pelo
efeito de desvio da luz pelo Sol previsto pela
relatividade geral, e que
é de 1,7 segundos de arco na borda do Sol, e 4 mili-segundos de
arco a 90° do Sol.
Mesmo com esta precisão só é possível medir paralaxes de objetos a 1600 anos-luz
de distância, cerca de 1 centésimo do tamanho da nossa Galáxia.
Em 2013 a Agência Espacial Européia lançou o satélite Gaia, para
medir a posição de estrelas com precisão
de 24 microsegundos de arco, tamanho de uma moeda de um real na Lua, vista da Terra.
Em 14 de setembro de 2016 começaram a sair os primeiros resultados da missão,
com a paralaxe de 2 milhões de estrelas, e em 13 de junho de 2022 o
Data Release 3 publicou a paralaxe de 1,6 bilhão de estrelas até magnitude 21.
Até poucos anos, com os telescópios disponíveis na Terra,
a maior distância de estrelas que se podia medir com precisão melhor do que
10% era 20 pc, que corresponde a paralaxes ≤ 0,05′′
O uso de CCD e telescópios dedicados reduziu a incerteza das observações na Terra para até 1 mili-segundo de arco, similar à incerteza das medidas do
satélite HIPPARCOS (High-Precision Parallax Collecting Satellite),
construído para medir com alta
precisão a posição e a paralaxe
de 120 000 estrelas. Ele foi lançado em agosto de 1989 e operou
com sucesso por 3 anos, apesar de não ter alcançado a
órbita geoestacionária pretendida. É importante notar
que 1 mili-segundo de arco é equivalente
ao tamanho angular de uma pessoa na superfície da Lua vista da Terra.
Para atingir esta precisão, foi necessário corrigir pelo
efeito de desvio da luz pelo Sol previsto pela
relatividade geral, e que
é de 1,7 segundos de arco na borda do Sol, e 4 mili-segundos de
arco a 90° do Sol.
Mesmo com esta precisão só é possível medir paralaxes de objetos a 1600 anos-luz
de distância, cerca de 1 centésimo do tamanho da nossa Galáxia.
Em 2013 a Agência Espacial Européia lançou o satélite Gaia, para
medir a posição de estrelas com precisão
de 24 microsegundos de arco, tamanho de uma moeda de um real na Lua, vista da Terra.
Em 14 de setembro de 2016 começaram a sair os primeiros resultados da missão,
com a paralaxe de 2 milhões de estrelas, e em 13 de junho de 2022 o
Data Release 3 publicou a paralaxe de 1,6 bilhão de estrelas até magnitude 21.
Exemplo:
| Estrela | Paralaxe | Distância | |
|---|---|---|---|
| Próxima Centauri | 0,772" | 1,295 pc | 4,223 a.l. |
| Sírius | 0,379" | 2,638 pc | 8,606 a.l. |
| Procyon | 0,286" | 3,496 pc | 11,404 a.l. |
![]() Estrelas Binárias
Estrelas Binárias
![]() Fotometria
Fotometria
![]() Astronomia e Astrofísica
Astronomia e Astrofísica