Até Newton publicar o Principia em 1687, mesmo Galileo pensava que as marés eram causadas pela rotação da Terra. Depois do Principia, todos aceitaram que a gravidade causa o deslocamento dos oceanos na direção do Lua e do Sol. O primeiro estudo sistemático das marés na Terra foi a Teoria de Equilíbrio, estabelecida pela teoria da gravidade de Newton, que explica que a gravitação lunar e solar causa uma deformação elipsoidal nos oceanos, sem considerar a complexidade causada pela rotação e pela geografia dos continentes. Lord Kelvin estabeleceu a teoria de hidráulica. Depois Bernoulli, em 1740, seguido de Laplace em 1775, refinaram a matemática e a física de ondas em uma Teoria Dinâmica de Marés, que levava em conta a interação das forças celestes e da interrupção dos movimentos de marés pelos continentes em um planeta em rotação, bem como a hidráulica sobre as placas continentais. O modelo atual para o cálculo das marés chama-se Teoria Harmônica, e foi desenvolvido pelos oceanógrafos ingleses Arthur Thomas Doodson (1890-1968) ["The Harmonic Development of the Tide-Generating Potential", Proceedings of the Royal Society of London. Series A, Vol. 100, No. 704 (Dec. 1, 1921), pp. 305-329] e Joseph Proudman (1888-1975) ("The Dynamical Theory of Tides", 1923). Esta teoria calcula as marés como uma soma de um número finito (37 nas tabelas atuais) componentes sinusoidais independentes, com as frequências determinadas pelas forças astronômicas, mas as amplitudes dadas pelos efeitos oceanográficos, hidráulica de águas rasas e geografia da costa. Nosso interesse neste capítulo é somente descrever as forças astronômicas.
Corpos com simetria esférica agem, gravitacionalmente, como massas pontuais (Teorema das Cascas Esféricas, Isaac Newton, Philosophiae Naturalis Principia Mathematica, Londres, 1687, Theorem XXXI), para as quais as influências gravitacionais são facilmente calculadas. Na natureza, no entanto, os corpos na maioria das vezes não são perfeitamente esféricos. Alexis Claude Clairaut (1713-1765), em seu livro de 1743, A Teoria da Forma da Terra, estudando o equilíbrio de fluídos e a força gravitacional em elipsóides em revolução, concluiu que a Terra não é esferica, mas um elipsoide achatado nos polos. Juntamente com o matemático francês Pierre Louis Moreau de Maupertuis (1698-1759), Clairaut foi em uma expedição para a Lapônia (67°N, círculo polar norte), na Finlândia, em 1735 para medir este achatamento. Se a Terra fosse perfeitamente esférica, um grau medido verticalmente ao longo do meridiano deveria ser o mesmo em todos os pontos da Terra. Eles demonstraram que esta distância era maior próximo ao polo. O diâmetro equatorial é 12,756,3 km, enquanto o diâmetro polar é 12.713,5 km. A diferença de 42,8 km deve-se ao fato da Terra ter a forma de um geoide. A principal contribuição à não esfericidade em planetas vem das forças gravitacionais diferenciais que corpos vizinhos exercem uns nos outros. Essas forças diferenciais resultam em fenômenos como marés e precessão.
A força total exercida sobre uma partícula de um corpo extenso será:
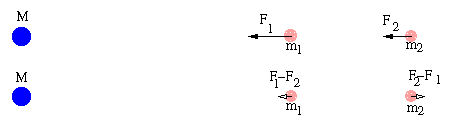
A força diferencial 
tende a
separar as
duas partículas m1 e m2
pois, em relação ao centro de massa, as
duas se afastam. Se as duas partículas são parte do mesmo corpo,
a força diferencial tende a alongá-lo ou mesmo rompê-lo.
