Isaac Newton

Estudando o movimento dos corpos, Galileo Galilei (1564-1642) descobriu através de experimentos que "um corpo que se move, continuará em movimento a menos que uma força seja aplicada e que o force a parar." Galileo argumentou que o movimento é tão natural quanto o repouso, isto é, um corpo que está em repouso permanece em repouso a menos que seja submetido a uma força que o faça mover-se. Se um objeto já está se movimentando, ele continuará em movimento a menos que seja submetido a uma força que o faça parar.

Galileo descobriu os satélites de Júpiter e comunicou seus dados a Johannes Kepler (1571-1630), que os observou pessoalmente. Os satélites obedecem às Três Leis de Kepler, porém com um valor da constante k diferente na 3^a Lei (P²=k a³).

Sessenta anos depois, o inglês Isaac Newton (1643-1727) foi quem deu uma explicação completa ao movimento e à forma como as forças atuam. A descrição está contida nas suas 3 leis:

Primeira Lei: Inércia, é baseada na enunciada por Galileo, embora Galileo não tenha realmente chegado ao conceito de inércia. Na ausência de forças externas, um objeto em repouso permanece em repouso, e um objeto em movimento permanece em movimento, ficando em movimento retilíneo e com velocidade constante. Esta propriedade do corpo que resiste à mudança, chama-se inércia. A medida da inércia de um corpo é seu momentum. Newton definiu o momentum de um objeto como sendo proporcional à sua velocidade. A constante de proporcionalidade, que é a sua propriedade que resiste à mudança, é a sua massa:

$\vec p = m\vec v =$ constante se $\vec F = 0$

Segunda Lei: Lei da Força, relaciona a mudança de velocidade do objeto com a força aplicada sobre ele. A força líquida aplicada a um objeto é igual à massa do objeto vezes a aceleração causada ao corpo por esta força. A aceleração é na mesma direção da força.

$\vec F = m \times \vec a = m \times \frac{d\vec v}{dt} = \frac{d\vec p}{dt}$

Terceira Lei: Ação e Reação, estabelece que se o objeto exerce uma força sobre outro objeto, este outro exerce uma força igual e contrária.

Newton pôde explicar o movimento dos planetas em torno do Sol, assumindo a hipótese de uma força dirigida ao Sol, que produz uma aceleração que força a velocidade do planeta a mudar de direção continuamente. Como foi que Newton descobriu a Lei da Gravitação Universal? Considerando o movimento da Lua em torno da Terra e as leis de Kepler.

Aceleração em órbitas circulares: o holandês Christiaan Huygens (1629-1695), em 1673 e, independentemente, Newton, em 1665 (mas publicado apenas em 1687, no Philosophiae naturalis principia mathematica, 27 MB PDF) descreveram a aceleração centrípeta.

Consideremos uma partícula que se move em um círculo.
No instante t a partícula está em D, com velocidade na direção DE. Pela 1^a. lei de Newton, se não existe uma força agindo sobre o corpo, ele continuará em movimento na direção DE.
Após um intervalo de tempo dt, a partícula está em G, percorreu a distância v.dt, e está com velocidade , de mesmo módulo v, mas em outra direção.
Consideremos infinitésimos: Δt = dt e Δv = dv.

Seja θ o ângulo entre o ponto D e o ponto G.
Mas θ também é o ângulo entre e , já que v₁ é perpendicular a OD e v₂ é perpendicular a OG. Portanto,

e, portanto, a aceleração a=dv/dt:

Se a partícula tem massa m, a força central necessária para produzir a aceleração é:

$F = m\frac{v^2}{r}$

Claramente a dedução é válida se e são extremamente pequenos e é um exemplo da aplicação do cálculo diferencial, que foi desenvolvido pela primeira vez por Newton [e simultaneamente por Gottfried Wilhelm von Leibniz (1646-1716)].

Gravitação Universal

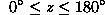
Obviamente a Terra exerce uma atração sobre os objetos que estão sobre sua superfície. Newton se deu conta de que esta força se estendia até a Lua e produzia a aceleração centrípeta necessária para manter a Lua em órbita. O mesmo acontece com o Sol e os planetas. Então Newton formulou a hipótese da existência de uma força de atração universal entre os corpos em qualquer parte do Universo.

A força centrípeta que o Sol exerce sobre um planeta de massa m, que se move com velocidade v à uma distância r do Sol, é dada por:

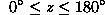$F = m\frac{v^2}{r}$                                                        (F_c)

Assumindo neste instante uma órbita circular, que mais tarde será generalizada para qualquer tipo de órbita, o período P   do planeta é dado por:

Pela 3^a Lei de Kepler,

P²=k r³

onde a constante k depende das unidades de P e r. Temos então que

Seja m a massa do planeta e M a massa do Sol. Substituindo-se esta velocidade na expressão da força centrípeta exercida pelo Sol (F_c) no planeta, a força pode então ser escrita como:

e, de acordo com a 3^a. lei de Newton, o planeta exerce uma força igual e contrária sobre o Sol. A força centrípeta exercida pelo planeta sobre o Sol, de massa M é dada por:

Newton deduziu então que:

onde G é uma constante de proporcionalidade e o sinal negativo é porque a força é atrativa. Tanto o Sol quanto o planeta que se move em torno dele experimentam a mesma força, mas o Sol permanece aproximadamente no centro do Sistema Solar porque a massa do Sol é aproximadamente mil vezes maior que a massa de todos os planetas somados.

Newton então concluiu que para que a atração universal seja correta, deve existir uma força atrativa entre pares de objetos em qualquer região do universo, e esta força deve ser proporcional a suas massas e inversamente proporcional ao quadrado de suas distâncias. A constante de proporcionalidade G depende das unidades das massas e da distância.

Derivação da "Constante" k

Suponha dois corpos de massas m₁ e m₂, separados do centro de massa por r₁ e r₂.
A atração gravitacional entre eles depende da distância total entre eles e é dada por:

$F_G=\frac{Gm_1m_2}{(r_1+r_2)^2}$

Já a aceleração centrípeta é dirigida ao centro de massa e é dada por:

$F_1 = \frac{m_1v_1^2}{r_1}$

e

$F_2 = \frac{m_2v_2^2}{r_2}$

Como estamos assumindo órbitas circulares e, por definição de centro de massa, os períodos têm que ser os mesmos, ou o centro de massa se moveria, temos:

e similarmente para m₂. Para que os corpos permaneçam em órbitas, as forças precisam ser idênticas:

e

Eliminando-se na primeira e na segunda e somando-se, obtemos:

ou:

$P^2 = \frac{4\pi^2}{G(m_1+m_2)}(r_1+r_2)^3$

Identificando-se a como a separação entre os corpos, a=(r₁+r₂), e escrevendo P²=Ka³, obtemos:

$${K = \frac{4\pi^2}{G(m_1+m_2)}}$$ (1)

Isso nos diz que a "constante" K, definida como a razão $\frac{P^2}{a^3}$, só é constante realmente se $(m_1+m_2)$ permanece constante. Isso é o que acontece no caso dos planetas do Sistema Solar; como todos planetas têm massa muito menor do que a massa do Sol, já que o maior planeta, Júpiter, tem quase um milésimo da massa do Sol, a soma da massa do Sol com a massa do planeta é sempre aproximadamente a mesma, independente do planeta. Por essa razão Kepler, ao formular sua 3^a lei, não percebeu a dependência com a massa.

Mas, se considerarmos sistemas onde os corpos principais são diferentes, então as razões $\frac{P^2}{a^3}$ serão diferentes. Por exemplo, todos os satélites de Júpiter têm praticamente a mesma razão $\frac{P^2}{a^3} = K_J$, que portanto podemos considerar constante entre elas, mas essa constante é diferente da razão $\frac{P^2}{a^3}= K_\odot$ comum aos planetas do Sistema Solar.

Determinação de massas

A terceira lei de Kepler na forma derivada por Newton pode se escrita como:

$${(M + m) = \frac{4\pi^2}{G}\,\frac{a^3}{P^2}}$$ (3)

que nada mais é do que a última parte da Terceira Lei, onde foi substituído $K$ por $\frac{{P}^2}{{a}^3}$.

No sistema internacional de unidades, G = (6,67428 ± 0,00067) × 10^-11 N m²/kg², e foi medida em laboratório pelo físico inglês Henry Cavendish (1731-1810) em 1798 [Philosophical Transactions (part II) 88, p.469-526 (21 Junho 1798)], usando uma balança de torsão. Mas, em astronomia, muitas vezes é mais conveniente adotar outras unidades que não as do sistema internacional. Por exemplo, em se tratando de sistemas nos quais o corpo maior é uma estrela, costuma-se determinar suas massas em unidades de massa do Sol, ou massas solares (massa do Sol = $M_\odot$), seus períodos em anos e suas distâncias entre si em unidades astronômicas. Em sistemas em que o corpo maior é um planeta, é conveniente expressar sua massa em unidades de massas da Terra (massa da Terra = $M_\oplus$), seu período em meses siderais e suas distâncias relativas em termos da distância entre Terra e Lua. Nestes sistemas particulares, a terceira lei de Kepler pode ser escrita como

$M + m = \frac{a^3}{P^2}$

a qual é especialmente útil para a determinação de massas de corpos astronômicos. Note que esta fórmula só pode ser aplicada assim nestas unidades:

1. massas em massas solares, período em anos e a em Unidades Astronômicas
2. massas em massas terrestres, período em meses siderais (27,33 dias) e a em distância Terra-Lua

Por exemplo, se se observa o período orbital e a distância de um satélite a seu planeta, pode-se calcular a massa combinada do planeta e do satélite, em massas solares ou massas terrestres. Como a massa do satélite é muito pequena comparada com a massa do planeta, a massa calculada $(m + M)$ é essencialmente a massa do planeta $(M)$.

Da mesma forma, observando-se o tamanho da órbita de uma estrela dupla, e o seu período orbital, pode-se deduzir as massas das estrelas no sistema binário. De fato, pode-se usar a terceira lei de Kepler na forma revisada por Newton para estimar a massa de nossa Galáxia e de outras galáxias.

Exemplos de uso da 3^a lei de Kepler

Exemplo 1

Qual é a massa do Sol? Sabemos que a Terra orbita o Sol em 1 ano. Podemos usar a relação

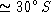P² = (r₁ + r₂)³

e lembrar que a = r₁ + r₂ = 1 UA = 1,5 ×10¹¹ m. Reescrevendo:

(m₁ + m₂) = ${\frac{4\pi^2 a^3}{GP^2}}$

Como G = 6, 67×10^-11 m³ kg^-1 s^-2 e P= 1 ano = 3,16×10⁷ s, obtemos

m_Sol + m_Terra = = 2×10³⁰ kg

Exemplo 2:

Deimos, o menor dos 2 satélites de Marte, tem período sideral de 1,262 dias e uma distância média ao centro de Marte de 23500 km. Qual a massa de Marte?

Podemos resolver este problema de diversas maneiras. Aqui vamos mostrar algumas delas.

1. Calculando a massa de Marte diretamente em massas terrestres. (Vamos usar a notação: Marte = Ma; Deimos = D; Terra = $\oplus$ e Lua = L).
   1. Uma maneira de resolver o problema é compararando os parâmetros da órbita de Deimos em torno de Marte com os parâmetros da órbita da Lua em torno da Terra, sem introduzir o valor da constante.

      Desprezando a massa de Deimos e da Lua frente às massas de seus respectivos planetas, podemos escrever:

      M_MaK_Ma = M_$\oplus$K_$\oplus$
      sendo K_Ma = (P_D)²/(a_D)³

      e K_$\oplus$ = (P_L)²/(a_L)³

      Então:

      ${\frac{{M_{Ma}}}{{M_{\oplus}}}}$ = ${\frac{{{(P_{L})}^2 /{(a_{L})^3}}}{{ {(P_{D})}^2/({a_D)}^3}}}$ = $\left(\vphantom{\frac{P_L}{P_D}}\right.$${\frac{{P_L}}{{P_D}}}$$\left.\vphantom{\frac{P_L}{P_D}}\right)^{{2}}_{{}}$$\left(\vphantom{\frac{a_D}{a_L}}\right.$${\frac{{a_D}}{{a_L}}}$$\left.\vphantom{\frac{a_D}{a_L}}\right)^{{3}}_{{}}$
      Sabendo que:

      P_L = 27, 32 dias

      P_D = 1, 262 dias

      a_L = 384 000 km

      a_D = 23 500 km

      Temos:

      ${\frac{{M_{Ma}}}{{M_{\oplus}}}}$ = $\left(\vphantom{\frac{27,32\, {dias}}{1,262\,{dias}}}\right.$${\frac{{27,32\, {dias}}}{{1,262\,{dias}}}}$$\left.\vphantom{\frac{27,32\, {dias}}{1,262\,{dias}}}\right)^{{2}}_{{}}$$\left(\vphantom{\frac{23500\, {km}}{384000\,{km}}}\right.$${\frac{{23500\, {km}}}{{384000\,{km}}}}$$\left.\vphantom{\frac{23500\, {km}}{384000\,{km}}}\right)^{{3}}_{{}}$ = 0, 1
      ${ M_{Ma} = 0,1\, M_{\oplus}}$
   2. Podemos chegar ao mesmo resultado usando a expressão formal da 3.a lei de Kepler (equação 1.3), escrevendo as distâncias em termos da distância Terra-Lua, as massas em massas terrestres, e os períodos em termos do período da Lua, ou seja, usando o sistema de unidades [distância T-L (d_TL), massa terrestre (M_$\oplus$), mês sideral ( mes)]:
      M_Ma + m_D $\simeq$ M_Ma = ${\frac{{4 \pi^2}}{{G}}}$${\frac{{{({a_D})}^3}}{{{({P_D})}^2}}}$
      Fazendo as transformações de unidades:

      P_D = (1, 262/27, 32) meses = 4, 62×10^-2 meses

      a_D = (23500/384000) d_TL = 6, 1×10^-2 d_TL

      G = 4$\pi^{2}_{}$ (d_TL)³/(M_$\oplus$ meses²) $\Longrightarrow$ ${\frac{{4 \pi^2}}{{G}}}$ = 1 (M_$\oplus$ meses²)/(d_TL)³

      Temos:

      M_Ma = ${\frac{{{\left({6,1 \times 10^{-2}}\right)}^3}}{{{\left({4,62 \times 10^{-2}}\right)}^2}}}$M_$\oplus$ $\Longrightarrow$ ${M_{Ma} = 0,1\, M_\oplus}$

2. Calculando diretamente a massa de Marte em massas solares (M_$\odot$).

   1. Compararando o movimento de Deimos em torno de Marte com o movimento da Terra em torno do Sol:
      M_MaK_Ma = M_$\odot$K_$\odot$
      onde K_$\odot$ = (P_$\oplus$)²/(a_$\oplus$)³

      e K_Ma = (P_D)²/(a_D)³

      Então:

      ${\frac{{M_{Ma}}}{{M_{\odot}}}}$ = ${\frac{{{(P_{\oplus})}^2 /{(a_{\oplus})^3}}}{{ {(P_{D})}^2/({a_D)}^3}}}$ = $\left(\vphantom{\frac{P_\oplus}{P_D}}\right.$${\frac{{P_\oplus}}{{P_D}}}$$\left.\vphantom{\frac{P_\oplus}{P_D}}\right)^{{2}}_{{}}$$\left(\vphantom{\frac{a_D}{a_\oplus}}\right.$${\frac{{a_D}}{{a_\oplus}}}$$\left.\vphantom{\frac{a_D}{a_\oplus}}\right)^{{3}}_{{}}$
      Sabendo que:

      P_$\oplus$ = 365, 25 dias

      P_D = 1, 262 dias

      a_$\oplus$ = 1, 5×10⁸ km = 1 UA

      a_D = 2, 35×10⁴ km

      Temos:

      ${\frac{{M_{Ma}}}{{M_{\odot}}}}$ = $\left(\vphantom{\frac{365,25\,{dias}}{1,262\,{dias}}}\right.$${\frac{{365,25\,{dias}}}{{1,262\,{dias}}}}$$\left.\vphantom{\frac{365,25\,{dias}}{1,262\,{dias}}}\right)^{{2}}_{{}}$$\left(\vphantom{\frac{2,35\times 10^4\,{km}}{1,5\times 10^8\, {km}}}\right.$${\frac{{2,35\times 10^4\,{km}}}{{1,5\times 10^8\, {km}}}}$$\left.\vphantom{\frac{2,35\times 10^4\,{km}}{1,5\times 10^8\, {km}}}\right)^{{3}}_{{}}$ = 3, 2×10^-7
      ${ M_{Ma} = 3,2\times 10^{-7}\, M_\odot}$
   2. Usando a equação 1.3 e adotando o sistema de unidades [UA, M_$\odot$, ano].
      M_Ma + m_D $\simeq$ M_Ma = ${\frac{{4 \pi^2}}{{G}}}$${\frac{{{a_{D}}^3}}{{{{P_D}^2}}}}$
      Fazendo a transformação de unidades:

      P_D = (1, 262/365, 25) anos = 3, 46×10^-3 anos

      a_D = (2, 35×10⁴/1, 5×10⁸) UA = 1, 57×10^-4 UA

      G = 4$\pi^{2}_{}$ UA³/(M_$\odot$ ano²) $\Longrightarrow$ 4$\pi^{2}_{}$/G = 1 (M_$\odot$ ano²)/UA³

      Temos:

      M_Ma = ${\frac{{{(1,57 \times 10^{-4})}^3}}{{{(3,46\times 10^{-3})^2}}}}$M_$\odot$ $\Longrightarrow$ ${M_{Ma}= 3,2 \times 10^{-7} M_\odot}$

3. Calculando diretamente a massa de Marte em quilogramas, ou seja, usando os sistema internacional [m, kg, s]
   M_Ma + m_D $\simeq$ M_Ma = ${\frac{{4 \pi^2}}{{G}}}$${\frac{{{({a_D})}^3}}{{{({P_D})}^2}}}$

   Escrevendo todos os dados em unidades do sistema internacional:

   P_D = 1, 262 dias = 1, 09×10⁵ s

   a_D = 23 500 km = 2, 35×10⁵ m

   G = 6, 67×10^-11 m³/(kg s²)

   Temos:

   M_Ma = ${\frac{{4 \pi^2}}{{6,67 \times 10^{-11}}}}$ ${\frac{{kg\,s^2}}{{m^3}}}$${\frac{{{(2,35 \times 10^5 m)}^3}}{{{(1,09 \times 10^5 s) }^2}}}$
   ${M_{Ma} = 6,4 \times 10^{23} \,{kg}}$

Exemplo 3: Duas estrelas idênticas ao Sol giram uma em torno da outra a uma distância de 0,1 UA. Qual o período de revolução das estrelas?

2M_$\odot$ = ${\frac{{{(0,1 UA)}^3}}{{P^2}}}$ $\Longrightarrow$ P = $\sqrt{{0,001 \over 2}}$ = 0, 022 anos

Segunda Lei de Kepler = Conservação do momentum angular

A área descrita por um corpo que se move é dada por:

Em um tempo dt:

O momentum angular é definido como:

$\ell=\vert\vec{r}\times m\vec{v}\vert=mr\frac{d\phi}{dt}r=mr^2\frac{d\phi}{d t}$

Portanto

$\frac{dA}{dt}=\frac{1}{2}\frac{\ell}{m}$

que é constante porque o momentum angular e a massa são constantes.

Um pouco mais de história:

Christiaan Huygens (1629-1695), na foto ao lado, que também construía seus telescópios, descobriu em 1655 o satélite Titan de Saturno, e que as "extensões laterais" de Saturno descobertas por Galileo em 1610 eram na verdade anéis ( De Saturni Luna Observatio Nova, 1656 e Sistema Saturnia, 1659). Em 1656 inventou o relógio de pêndulo, e o patenteou no ano seguinte. Em 1673 publicou o Oscillatorium Horologium, no qual explicou o movimento do pêndulo e descreveu a força centrípeta.

Em sua próprias palavras, Newton, como citado no prefácio do catálogo dos Portsmouth Papers, descreve como utilizou as Leis de Kepler para derivar a gravitação universal. "In the year 1665, I began to think of gravity extending to the orb of the Moon, and having found out how to estimate the force with which [a] globe revolving within a sphere presses the surface of the sphere, from Kepler's Rule of the periodical times being in a sesquialterate proportion of their distances from the centers of their orbs I deduced that the forces which keep the Planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her orb with the force of gravity at the surface of the earth, and found them answer pretty nearly."

Em 1668 Newton construiu um telescópio refletor, usado atualmente em todos os observatórios profissionais, com um espelho curvo ao invés de uma lente, usadas nos telescópios refratores de Galileo e Kepler. O telescópio de Galileo, construído em 1609 era composto de uma lente convexa e uma lenta côncava. Kepler, no livro Diopitrice, publicado em 1611, explicou que seria melhor construir um telescópio com duas lentes convexas, como se usa atualmente. A explicação de Newton da decomposição da luz branca, mostrando que a luz branca é a combinação de luz de cores diferentes, cada uma com seu indice de refração, é a base da espectroscopia.

Leis de Kepler Generalizadas
Astronomia e Astrofísica