




Próxima: Binárias Próximas
Volta: Interiores Estelares
Anterior: Formação Estelar
Estrelas Binárias
Um grande número de estrelas está em sistemas binários e
múltiplos
A fração de binárias aumenta com a massa das estrelas
(Gaspard Duchêne & Adam Kraus, 2013, Stellar Multiplicity,
Annual Review of Astronomy and Astrophysics, 51, 269), passando de 27±1% para estrelas M (Jennifer G. Winters et al. 2019, Astronomical Journal, 157, 216), 41±2% para estrelas FGK e
alcançando mais de 70% para estrelas tipo B e O
(Hugues Sana et al. 2012,
Binary interaction dominates the evolution of massive stars,
Science 337, 444), com um modesta redução conforme a metalicidade aumenta (Haibo Yuan et al. 2014, Astrophysical Journal, 799;
Cristine N. Mazzola et al.
2020, Monthly Notices of the Royal Astronomical Society, 449, 1607).
A evolução das estrelas em sistemas múltiplos depende não somente da massa da estrela e sua composição química, mas também da separação entre elas.
Se as estrelas estão separadas
mais do que 10× o raio que terão quando supergigantes,
suas evoluções são como as de estrelas não binárias. Para distâncias
menores, existe interação entre as estrelas que afeta sua evolução.
Consideremos duas estrelas de massa
M1
e
M2
separadas por uma distância
a
orbitando o centro
de massa do sistema.
A solução geral do problema de três corpos é caótica, mas podemos calcular as soluções estáticas do sistema
que mantém a separação entre os três corpos constante, chamados de Pontos de Lagrange [Joseph-Louis Lagrange=Giuseppe Lodovico Lagrangia (1736-1813)].
No sistema de referência em rotação com o sistema binário,
o movimento de uma partícula de massa
m
é dado pela
relação:
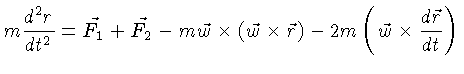 |
(1.126) |
onde 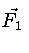 e
e 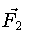 são as forças gravitacionais
sobre
m
causadas pelas estrelas de massas
são as forças gravitacionais
sobre
m
causadas pelas estrelas de massas 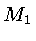 e
e 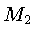 ,
e os dois últimos termos na equação (1.126)
representam a força centrífuga e a força de
Coriolis [Gustav-Gaspard Coriolis (1792-1843)].
A origem do sistema em rotação é o centro
de massa do sistema e
,
e os dois últimos termos na equação (1.126)
representam a força centrífuga e a força de
Coriolis [Gustav-Gaspard Coriolis (1792-1843)].
A origem do sistema em rotação é o centro
de massa do sistema e
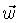 é a velocidade orbital
angular do sistema, apontando na direção perpendicular ao plano da órbita, que definimos como eixo z.
Estes termos precisam ser incluídos por que o sistema não é inercial.
é a velocidade orbital
angular do sistema, apontando na direção perpendicular ao plano da órbita, que definimos como eixo z.
Estes termos precisam ser incluídos por que o sistema não é inercial.
A força centrífuga pode ser derivada do potencial
Como a força de Coriolis é perpendicular à
direção de movimento, ela não pode realizar
trabalho sobre a massa pontual
m.
Se
m
está no plano (x,y), sua energia é dada por
e
O potencial V(x,y,0) tem máximos em três pontos críticos
no eixo x,
e dois no eixo y.
Esses pontos são chamados de pontos Lagrangianos.
Como são pontos de máximos,
podem ser
calculados calculando-se dV/dx=0 e dV/dy=0.
Seja R a distância entre o centro de massa e M2
Para o sistema Terra-Sol, α≃3×10-6, R=150 milhões de km, e os pontos L1 e L2 estão a aproximadamente 1,5 milhão de km da Terra.
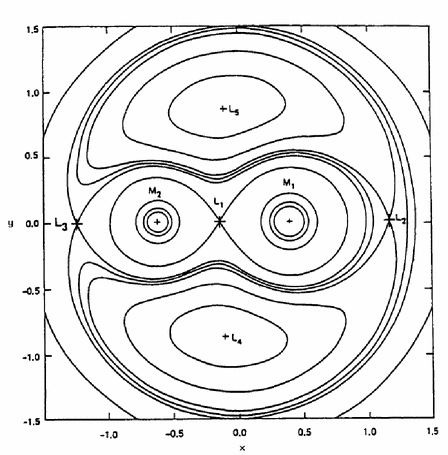 Equipotenciais de um sistema binário de massas similares,
mostrando os 5 pontos lagrangianos: L1 a L5. A equipotencial
que passa por L1 chama-se Lóbulo de Roche e, quando uma estrela
se expande até essa equipotencial, transfere massa para a companheira.
Equipotenciais de um sistema binário de massas similares,
mostrando os 5 pontos lagrangianos: L1 a L5. A equipotencial
que passa por L1 chama-se Lóbulo de Roche e, quando uma estrela
se expande até essa equipotencial, transfere massa para a companheira.
O ponto Lagrangiano
L1,
localizado no eixo x,
entre as duas estrelas, é de particular importância porque
se uma das estrelas se expande suficientemente tal que parte de
sua superfície atinge o ponto
L1,
ocorrerá transferência de
massa entre as estrelas. A curva equipotencial que inclui o ponto L1
é chamada de lóbulo de Roche
[Edouard Roche (1820-1883)].
As equipotenciais próximas de M1 e M2
são quase
esféricas em torno das estrelas individuais, enquanto
que as equipotenciais externas ao lóbulo de Roche envolvem
as duas estrelas.
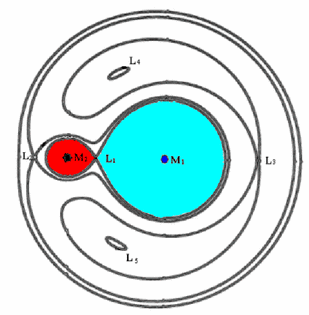 Equipotenciais de um sistema binário de massas diferentes.
Equipotenciais de um sistema binário de massas diferentes.
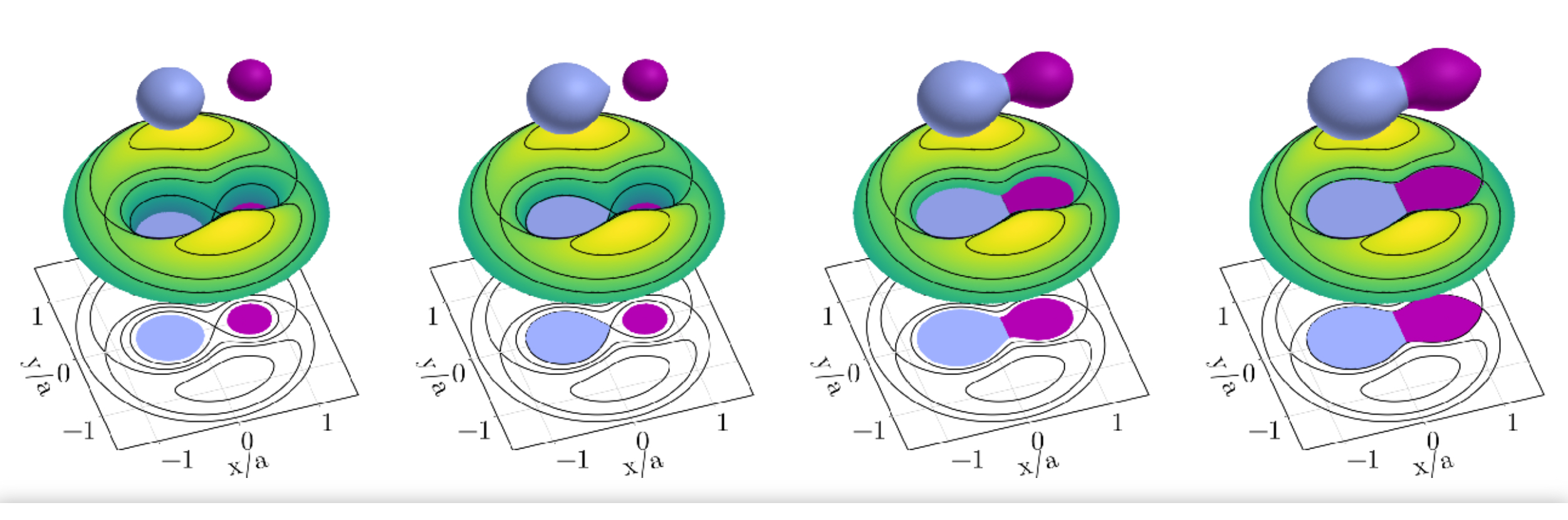
Os sistemas binários podem estar separados (
detached), quando as duas estrelas estão dentro do seus lóbulos de Roche,
preenchendo um lóbulo de Roche (
semi-detached), com deformações de maré levando a variações elipsoidais na curva de luz,
em contato,
preenchendo os dois lóbulos de Roche, formando um
envelope comum, quando há gás das duas estrelas fora dos seus lóbulos de Roche, ou perdendo matéria pelo L
2 (
overflow)
(Pablo Marchant, 2025, Evolution of binary stars).
Pela Terceira Lei de Kepler
Consideremos um sistema com duas estrelas de sequência principal, uma com M1=1 M⊙ e outro com 0,5 M⊙.
A soma dos raios das estrelas é R1+R2≃1,5 R⊙. O período orbital mínimo, para as estrelas não colidirem, é P ≥ 4,08 h,
assumindo uma órbita circular, como na equação acima. Entretanto, quando as duas estrelas estavam na pré-sequência principal, queimando deutério, a soma dos raios era R1+R2≃12 R⊙,
e o período orbital mínimo era P ≥ 4 dias. Depois de cerca de 10 G anos, a estrela de 1 M⊙ crescerá em uma gigante vermelha e, antes do flash de hélio, terá aproximadamente
R1≃170 R⊙, e sua massa terá reduzido para aproximadamente 0,8 M⊙, com período orbital mínimo de P ≥ 200 dias.
Embora a distribuição de períodos orbitais observados seja log-normal (log P tem distribuição normal),
com períodos médios de 300 anos para estrelas tipo G e 1600 dias para estrelas tipo espectral M,
alguns sistemas binários eclipsantes com duas estrelas de sequência principal têm períodos orbitais de somente 5 horas, o que indica que algum mecanismo reduziu seu período orbital desde quando elas eram estrelas de pré-sequência principal.
Se uma estrela em um sistema binário preenche seu lóbulo de Roche devido à sua evolução, ela não pode mais permanecer em equilíbrio hidrostático, e há transferência de massa entre as componentes pelo ponto Lagrangiano L1.
Como exemplo, um modelo de 4 M⊙ tem um raio na sequência principal R≃2,3 R⊙,
quando sai da sequência principal R≃6,4 R⊙, na base do Ramo Gigante de R≃23 R⊙
e R≃63 R⊙ quando a queima do He se inicia. Este modelo tem um raio de R≃41 R⊙ quando termina a queima do He e R≃280 R⊙
quando chega ao topo do Ramo Gigante Assintótico.
Betelgeuse, α Orionis, é uma supergigante vermelha M1-2 Ia-ab, com 14 M⊙ e 887±203 R⊙.





Próxima: Binárias Próximas
Volta: Interiores Estelares
Anterior: Formação Estelar
 Astronomia
e Astrofísica
Astronomia
e Astrofísica

©
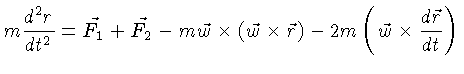
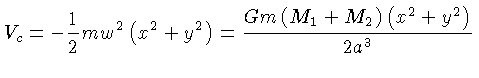
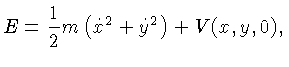
![$ - \frac{GmM_1}{[(x-x_1^2)^2+y^2]^{1/2}} - \frac{GmM_2}{[(x-x_2^2)^2+y^2]^{1/2}} -$](img966.gif)
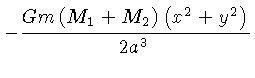
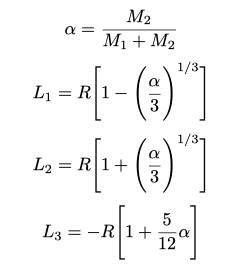



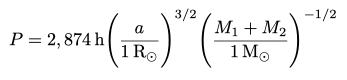
![]()