




Próxima: Transições Ligado-Livre
Volta: Interiores Estelares
Anterior: Abundância dos Elementos
A opacidade do material, com dimensões de área por unidade de massa, representa
a soma das secções de choque de todos os absorvedores e espalhadores em um dado volume,
divido pela massa deste volume.
Para tratar corretamente o transporte de energia por radiação,
precisamos dispor de valores da opacidade para todas as condições
de temperatura e densidade no interior estelar e mesmo na sua
atmosfera.
A maior parte da massa de uma estrela
na sequência principal está a temperaturas da
ordem de 1 a 30 × 106 K. A essas temperaturas, o pico da
distribuição de Planck varia entre 29 Å e 0,9 Å,
de acordo com a Lei de Wien

Esses comprimentos de onda correspondem a raio-X, mole e duro.
A essas temperaturas todos os elementos estão ionizados a tal
ponto que no máximo alguns elétrons permanecem nas
camadas mais internas. O hidrogênio e o hélio estão
essencialmente ionizados e, portanto, estão na forma
de elétrons, prótons e partículas
α, livres.
O pico da distribuição de Planck ocorre em hνmax=2,82 kT. Para T≫60 000 K, tanto o H quanto o He estão
totalmente ionizados, já que a ionização do H ocorre com 13,6 eV, a primeira do He a 24,6 eV e a segunda do He a 54,4 eV.
Mas os outros elementos só estão completamente ionizados a temperaturas muito mais altas. Para um átomo hidrogênico de número atômico Zi, isto é, com só um
elétron ligado, a energia de ionização é I=Zi2(13,6 eV). Portanto para remover o último elétron do oxigênio requer uma energia de
870 eV e, portanto, o O está metade ionizado para T1/2∼0,1 I/k≃106 K, pela lei de Saha, enquanto o ferro, com ZFe=26, requer
I=9200 eV, levando a uma temperatura de metade de ionização a T1/2∼0,1 I/k≃107 K. Por isto a base da zona
de convecção do Sol, em r≃=0,71 R⊙ e T≃2×106 K tem alta opacidade de Fe.
Raio elétron = 2,817 940 3205×10-15 m
Raio Bohr = 5,291 772 105 44×10-11 m = 18 782 Re → σB=352 778 σe
Raio Fe = 1,26×10-10 m = 2,38×RB
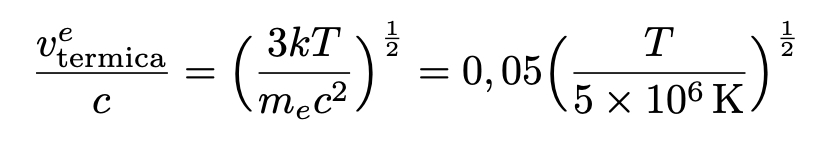
Na nossa definição de opacidade, a absorção da
radiação quando atravessa uma unidade de massa em uma
coluna de área perpendicular unitária e
altura ds
é
dada por:
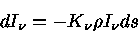 |
(28) |
logo
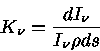 |
(29) |
isto é, a opacidade é a fração absorvida da radiação
atravessando uma coluna de altura
ds.
A profundidade ótica τν, definida como
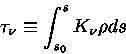 |
(30) |
representa a distância para a qual a intensidade decai de um fator
e,
e
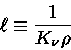 |
(31) |
pode ser interpretado como o livre caminho médio dos fótons.
No núcleo das estrelas, três mecanismos geram a opacidade:
- absorção verdadeira
- transições ligado-ligado (absorção em linhas, excitação)
- transições ligado-livre (ionização)
- transições livre-livre (bremstrahlung:
um elétron livre no campo
de um íon pode absorver ou perder uma quantidade arbitrária de energia,
e aumentar ou reduzir sua energia cinética).
- espalhamento Thomson
[Sir Joseph John Thomson (1856-1940)] de fótons por
elétrons livres, clássicos
→ se o elétron não adquirir
velocidade relativística (kT≪mec2), chama-se
efeito Compton coerente (quântico)
[Arthur Holly Compton (1892-1962)].
O termo coerente implica que a reemissão é na mesma frequência
da radiação incidente. Se os elétrons forem relativísticos,
a reemissão é incoerente.
Esse processo, embora não seja uma
absorção real, atenua o feixe de radiação, porque
o elétron re-irradia, ou espalha, a luz em outra direção.
- atenuação com absorção insignificante,
devido à dispersão. Por exemplo, reflexão. Essa atenuação
é normalmente desprezível, e assumimos o índice
de refração
μν=1. Essa aproximação não é
válida se o plasma for não-transmissivo ou na presença de
campo magnético. No caso geral
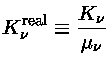 |
(1) |
Na região de baixas temperaturas (T ≤ 10 000 K), outros
processos físicos são importantes:
- absorção por íons negativos;
- absorção molecular;
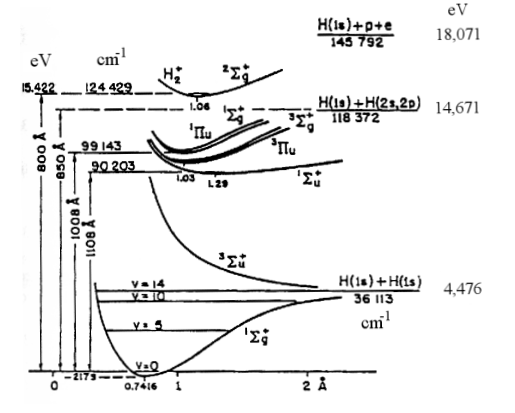 Diagrama dos níveis de energia da molécula H2.
As energias estão medidas a partir do estado fundamental.
Diagrama dos níveis de energia da molécula H2.
As energias estão medidas a partir do estado fundamental.
- espalhamento Rayleigh [Lord Rayleigh, John William Strutt (1842-1919)]
(absorção da radiação por uma molécula, indo
para um estado excitado e subseqüente reemissão
em qualquer direção);
- espalhamento Raman [Chandrasekhara Venkata Raman (1888-1970)]
(absorção da radiação por uma molécula, indo
para um estado excitado e subseqüente emissão
de radiação em outra frequência, pois a molécula
passa para um outro estado vibracional ou rotacional).
A energia de uma molécula, além do valor quântico principal
E0,
tem números quânticos rotacionais k
e vibracionais v:
onde I é o momento de inércia e w a frequência
angular fundamental de vibração.
- foto-excitação para estados auto-ionizantes [se
dois elétrons,
após absorverem radiação, estão excitados a níveis
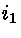 e
e 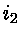 com energia de excitação
com energia de excitação
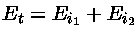 maior do que a energia de ionização, eles podem
fazer uma transição sem emissão de radiação,
para um estado de mesma energia total, mas com um elétron
removido (ionizado)];
maior do que a energia de ionização, eles podem
fazer uma transição sem emissão de radiação,
para um estado de mesma energia total, mas com um elétron
removido (ionizado)];
- absorção por grãos de poeira.
Para altíssimas temperaturas (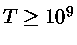 K), importantes nos núcleos de
estrelas evoluídas:
K), importantes nos núcleos de
estrelas evoluídas:
- produção de pares;
- espalhamento Compton incoerente (emissão em frequência diferente da incidente)
por elétrons relativísticos;
- absorção nuclear;
- espalhamento fóton-fóton;
- processos fóton-neutrinos.
Como os processos de absorção dependem da frequência,
e a estrutura da estrela não, normalmente se substitui
a opacidade na equação do equilíbrio
radiativo (1.51) pela sua média ponderada
definida como a opacidade média de Rosseland,
pelo norueguês Svein Rosseland (1894-1985) em 1924,
de modo que a equação do equilíbrio radiativo
seja válida para quantidade integradas sobre a frequência:
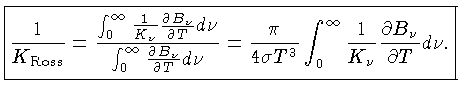 |
(1.62) |
Frequentemente se aproxima a opacidade por uma fórmula do tipo:
que embora não precisas, servem para estimativas. O caso
n=1 e s=3,5, válido para absorção livre-livre em
um gás não degenerado em que a maioria dos elementos
está completamente ionizado, é chamada de opacidade
de Kramers, pois foi derivada classicamente para as opacidades
livre-livre e ligado-livre pelo
físico holandês Hendrik Anthony Kramers (1894-1952) em 1923
(Philosophical Magazine, 46, 836).
 Para regiões completamente ionizadas, espalhamento Thomson
de elétrons livres é dominante, e a opacidade é
dada por n=s=0, como veremos a seguir.
Para regiões completamente ionizadas, espalhamento Thomson
de elétrons livres é dominante, e a opacidade é
dada por n=s=0, como veremos a seguir.





Próxima: Transições Ligado-Livre
Volta: Interiores Estelares
Anterior: Abundância dos Elementos
 Astronomia e Astrofísica
Astronomia e Astrofísica
 ©
©
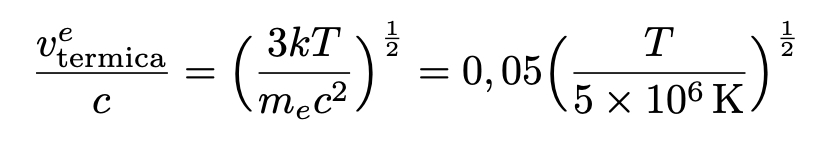
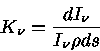
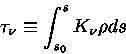
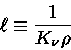
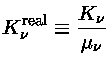

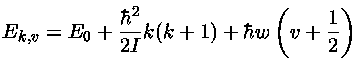
![]() K), importantes nos núcleos de
estrelas evoluídas:
K), importantes nos núcleos de
estrelas evoluídas:
 Para regiões completamente ionizadas, espalhamento Thomson
de elétrons livres é dominante, e a opacidade é
dada por n=s=0, como veremos a seguir.
Para regiões completamente ionizadas, espalhamento Thomson
de elétrons livres é dominante, e a opacidade é
dada por n=s=0, como veremos a seguir.